Question

Given trapezoid KLMN with KL | LM is 15m long, ∠M=115° and the diagonal LN makes an angle of 35° with LM. Find the area of the trapezoid in square meters.

Answer 1

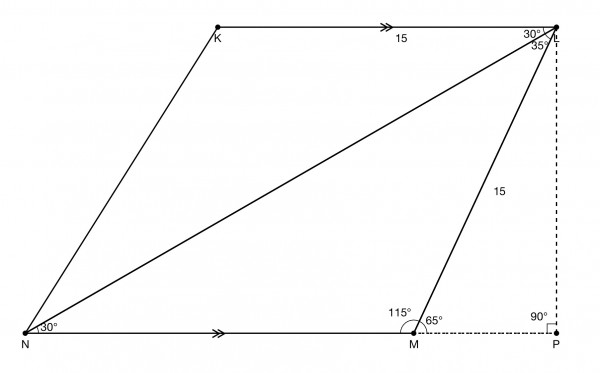
LP is the perpendicular from L to NM produced.

The area of the trapezoid is the sum of the areas of the triangles NKL and NLM. These triangles have the same height given by LP. A few extra angles are shown. Using the sine rule in triangle NLM:

15/sin30=15/(1/2)=30=NM/sin35, so NM=30sin35. LP/LM=sin65, so LP=15sin65, the common height of the triangles.

Area of triangle NKL=½15*15sin65; area of triangle NLM is ½30sin35*15sin65.

Therefore the area of KLMN is ½15sin65(15+30sin35)=½225sin65(1+2sin35)=218.9229 sq m approx.