PRQS is an isosceles trapezoid with median MD. If the measurement of angle SMD= 2(x+10) and measurement of angle RQP= 5x-16, what is the measurement of angle R

Question

What is the complete solution?

Answer 1

I assume the trapezoid is PQRS, not PRQS.

The angles at P, Q, M and D are all equal (congruent) because the trapezoid is isosceles and we have corresponding angles on a transverse between parallel lines. Therefore SMD=RQP, so 2(x+10)=5x-16.

Expanding: 2x+20=5x-16, 20+16=5x-2x, 36=3x, so x=12.

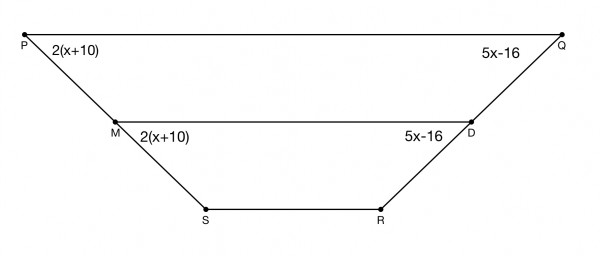
Now we know x we can find all the angles at the vertices:

Angles P and Q = 2(x+10)=44 degrees=5x-16 substituting x=12 degrees.

S and R are supplementary = 180-44=136 degrees.