The vertex of the parabola y2 = x moves exponentially y = ex.

Question

find the sulution

Answer 1

The vertex of y²=x is at (0,0), which is not on the curve y=e^x, so we need an exponential function which passes through (0,0). y=e^x-1 is such an exponential function. If the vertex moves to a point (h,k) where k=e^h-1, then the equation of the parabola changes to (y-k)²=x-h, that is, (y-e^h+1)²=x-h. For example, when h=1, the equation becomes (y-e+1)²=x-1.

Below is a representation of the series of parabolas created by using the exponential trajectory of the vertex.

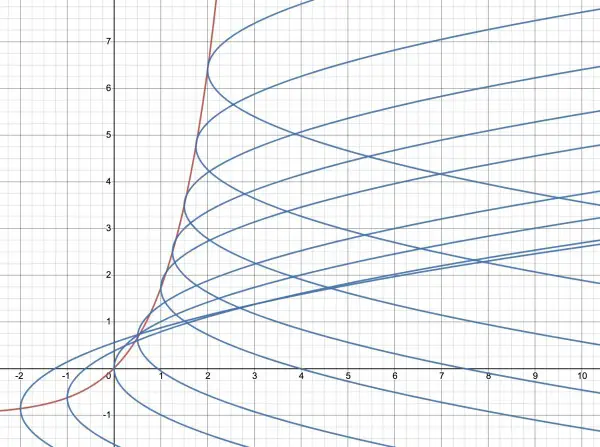
The red curve is y=e^x-1 and the series of parabolas is shown in blue.