The equation of the circle can be written (x+3)^2+(y+1)^2=16 by completing squares for x and y. From this (y+1)^2=16-(x+3)^2. The centre of the circle is at (-3,-1) and the radius is 4.
Differentiating wrt x we get: 2(x+3)+2(y+1)y'=0 so y'=-(x+3)/(y+1). This is the gradient at point (x,y), so since the gradient of the tangent has to be 1, because y=x+k has a gradient of 1, y'=1. If the point where the tangent line meets the circle is (p,q) then the tangent line is y-q=x-p so y=x+q-p and k=q-p.
-(p+3)/√(16-(p+3)^2)=1, being the gradient at (p,q) or (p,√(16-(p+3)^2)). Therefore -(p+3)=√(16-(p+3)^2); squaring both sides we have: (p+3)^2=16-(p+3)^2 and (p+3)^2=8, p=-3±2√2. From the standardised equation of the circle (q+1)^2=16-8=8 and q=-1±2√2. There are two points on the circle where the tangent line has a slope of 1 so there are two possible values for k (see picture). These points are diametrically opposite. The first point is when x is negative and y is positive (2nd quadrant) and the opposite point is when x is negative and y is negative (3rd quadrant). The points are (-3-2√2,-1+2√2) and (-3+2√2,-1-2√2), giving values of k=2+4√2, 2-4√2.
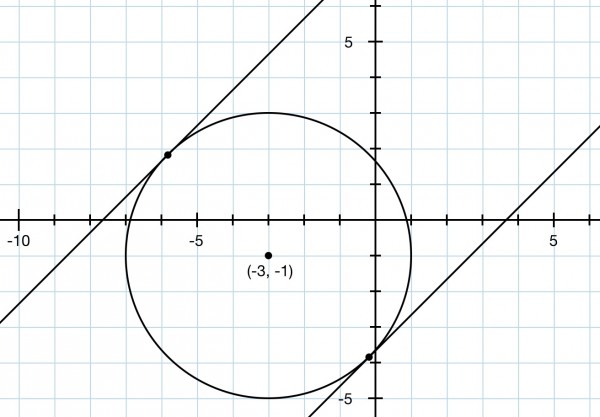
Note that the line y+1=x+3, that is, y=x+2 is the line passing through the circle's centre parallel to y=x+k. This line is equidistant from the two lines y=x+2+4√2 and y=x+2-4√2. From this fact it is possible to calculate the equations of the lines y=x+k for the two values of k without resorting to calculus. The two tangent points are radially distant from the centre by 4, at opposite ends of the diameter. The radius is the hypotenuse of an isosceles right-angled triangle, so the two sides have length a, given by 2a^2=4^2, making a=√8=2√2. The points on the circumference can then be calculated: y=-3±2√2 and x=-1±2√2. By plugging in the x-y values into y=x+k, or using slope-intercept form, the two values of k can be calculated: y+1-2√2=x+3+2√2, y=2+4√2; y+1+2√2=x+3-2√2, y=2-4√2.