y=Csmall1e raise to x+Csmall2cos2x+Csmall3sin2x

Question

solve for the differential equations with my given general solution

Answer 1

y=Csmall1e raise to x+Csmall2cos2x+Csmall3sin2x

rewriting this as,

y = C1.e^x + C2.cos(2x) + C3.sin(2x)

y' = C1.e^x - 2C2.sin(2x) + 2C3.cos(2x)

y'' = C1.e^x - 4C2.cos(2x) - 4C3.sin(2x)

 

y''              C1.e^x - 4C2.cos(2x) - 4C3.sin(2x)
+      =          +

4y            4C1.e^x + 4C2.cos(2x) + 4C3.sin(2x)

y'' + 4y = 5C1.e^x

The original DE from which your solution derives is: y'' + 4y = 5C1.e^x

Answer 2

y=C1e^x+C2cos(2x)+C3sin(2x).

When x=0, y=C1+C2. I assume C1, C2 and C3 are constants.

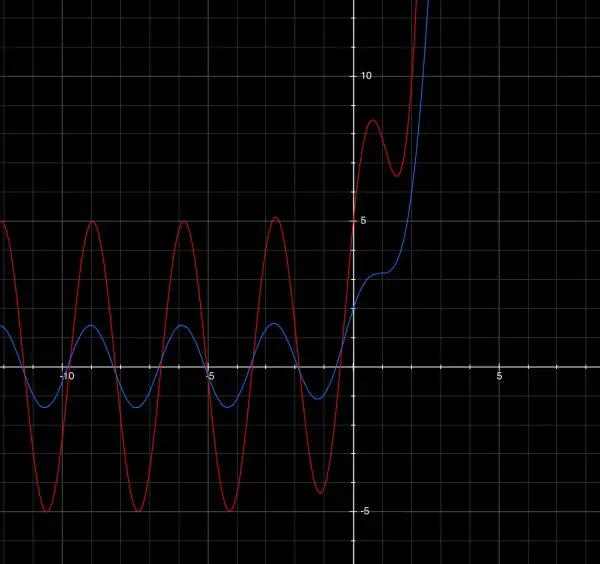
For the sake of illustration, let C1=2, C2=3 and C3=4, the red curve shown below.

Now let C1=C2=C3=1, the blue curve. The y-intercept for red is C1+C2=5 and for blue is C1+C2=2.

Note the contrast between negative values of x and positive values. This is because when x<0 the sine and cosine functions predominate since e^x is small; while when x>0 e^x predominates since sine and cosine are restricted to the range -1 to +1.