Question

A 22 kilos child is sitting at A(-7, -3) and a 47.5 kilos child is at B(1,4), where units are in feet. Find the point P between A and B which could be used as the fulcrum of a teeter board putting the two children in equilibrium.

Answer 1

For a general solution to this problem let A be the point (x1,y1) and B be (x2,y2). Let AB=R and let a on AB be the distance between A and the fulcrum F(x,y).

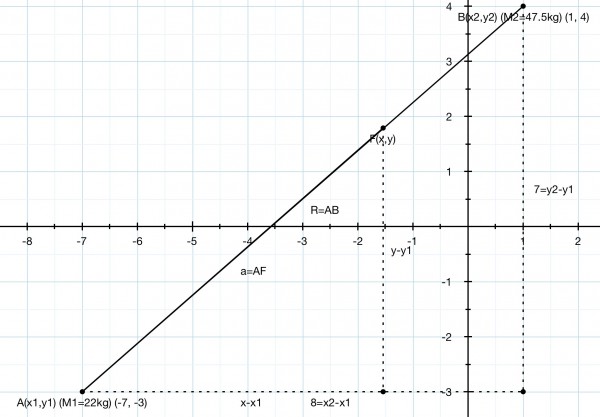
The masses are M1 at A and M2 at B. The moments about the fulcrum must be equal for equilibrium, so M1a=M2(R-a) and M1a+M2a=M2R, making a/R=M2/(M1+M2). By similar triangles (y-y1)/(y2-y1)=(x-x1)/(x2-x1)=a/R=M2/(M1+M2). Also, R=√(y2-y1)^2+(x2-x1)^2) and a=√(y-y1)^2+(x-x1)^2).

Therefore (x-x1)(M1+M2)=(x2-x1)M2; x(M1+M2)-x1M1-x1M2=x2M2-x1M2.

So x=(x1M1+x2M2)/(M1+M2) and y=(y1M1+y2M2)/(M1+M2).

Therefore the coordinates of F are ((x1M1+x2M2)/(M1+M2),(y1M1+y2M2)/(M1+M2)).

These formulae can be used in all problems of this nature.

We have M1=22kg and M2=47.5kg, so M1+M2=69.5kg.

x1=-7, y1=-3, x2=1, y2=4, so F is ((-7*22+47.5)/69.5,(-3*22+4*47.5)/69.5)=(-213/139,248/139)=(-1.53',1.78').

Note that the formula can be used to find any of the values M1, M2, x1, x2, x, y1, y2, y given the coordinates of A and B or F or M1 or M2.