in the diagram,ABCD is a rectangle.AB=12cm and BC=8cm.AP=BQ=CR=DS=x centimetres.find epression in terms of x,for the length QC and the area of triangle CRQ

Question

please help me to answer this question step by step

Answer 1

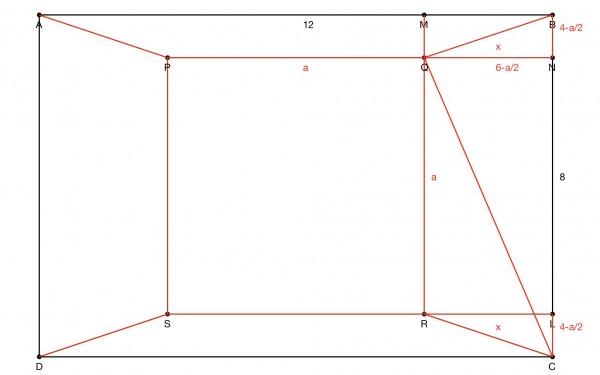
There is insufficient information about the points or figure PQRS, so I'm going to assume they form a square inside the rectangle ABCD. Because of symmetry, the centre of the square and rectangle coincide.

QM=BN=½(8-a)=4-a/2; QN=½(12-a)=6-a/2. NC=8-(4-a/2)=4+a/2.

By Pythagoras, QC^2=QN^2+NC^2=(6-a/2)^2+(4+a/2)^2 (1)

Also, by Pythagoras, QB^2=x^2=(4-a/2)^2+(6-a/2)^2 (2)

(1)-(2): QC^2-x^2=8a. From (2) x^2=52-10a+a^2/2.

So a^2-20a+104=2x^2; a^2-20a+100=2x^2-4; (a-10)^2=2x^2-4 and a=10±√(2x^2-4).

So QC=8(10±√(2x^2-4)).

Area of triangle CRQ=½QR.QN=a(6-a/2)/2=(5±√(2x^2-4)/2)(1T√(2x^2-4)/2).

Let y=√(2x^2-4)/2 then area=(5+y)(1-y) or (5-y)(1+y)=5-4y-y^2 or 5+4y-y^2, i.e., 5±4y-y^2.

This comes to 5±2√(2x^2-4)-(x^2/2-1)=6±2√(2x^2-4)-x^2/2.

If figure PQRS is not a square but only has one parameter (side a is a single parameter), the solution may nevertheless be a guide to the method.