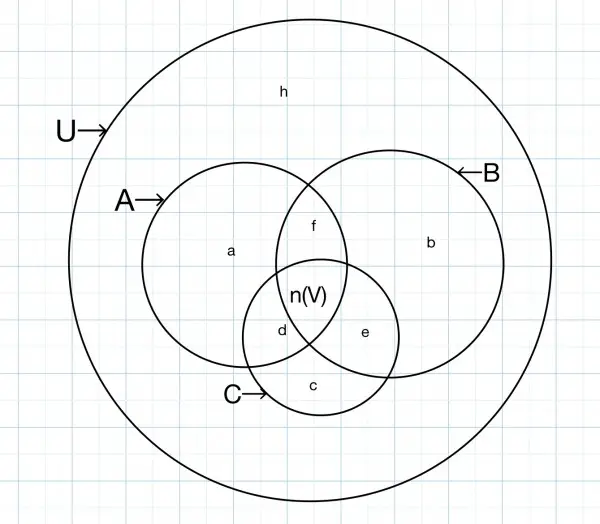
No diagram has been provided so the above Venn diagram is suggested because it contains 7 unknown regions labelled a, b, c, d, e, f, h. The assumed position of region V=A∩B∩C is shown and the number of elements in V is shown as n(V).
The complete regions A, B, C and U (the universal region) are shown as circles labelled by pointers.
Let g=n(V). We can now write all the intersections in terms of the numbers of elements in all 8 regions a-h.
n(A∩B)=f+g=8, n(A∩C)=d+g=11, n(B∩C)=e+g=5.
n(A)=a+d+f+g=22, n(B)=b+e+f+g=17, n(C)=c+d+e+g=17, n(U)=a+b+c+d+e+f+g+h=44.
The contents of each region can all be written in terms of g which has the given value of n(V).
f=8-g, d=11-g, e=5-g. From these equations we can see that g cannot be greater than 5.
a+d=14, b+e=9, c+d=12, a=14-(11-g)=g+3, b=9-(5-g)=g+4, c=12-(11-g)=g+1.
g+3+g+4+g+1+11-g+5-g+8-g+g+h=44, 32+g+h=44, g+h=12, h=12-g.
If n(V)=0, a=3, b=4, c=1, d=11, e=5, f=8, h=12
If n(V)=1, a=4, b=5, c=2, d=10, e=4, f=7, h=11
If n(V)=2, a=5, b=6, c=3, d=9, e=3, f=6, h=10
If n(V)=3, a=6, b=7, c=4, d=8, e=2, f=5, h=9
If n(V)=4, a=7, b=8, c=5, d=7, e=1, f=4, h=8
If n(V)=5, a=8, b=9, c=6, d=6, e=0, f=3, h=7
Note that only n(V)=0 and n(V)=3 give unique values for the number of elements in each of the 8 regions.