A soda company sells bottles and aluminum cans each bottling machine cost $40,000 per year requires. See moree info below for the rest of the question.

Question

A soda company sells bottles and aluminum cans. each bottling machine cost $40,000 per year requires four attendants and Bottles 150 cases per hour. each canning machine cost $60,000 per year requires three attendants and processes 250 cases per hour. the demand for soda in cans does not exceed 1,200 cases per hour the company wishes to process at least 2000 cases per hour and hire no more than 55 workers while the union insist that there be at least 45 workers and that their wages be $15,000 per worker per year. set up and solve a linear program to find the optimum number of machines the company should use in order to minimize their costs.

Answer 1

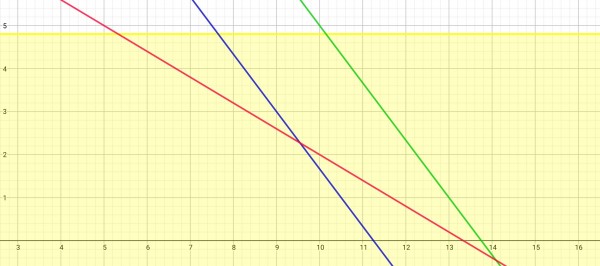
Let B=number of bottling machines and C=number of canning machines. In the picture, B is the horizontal axis and C the vertical axis.

Bottling cost=40000B+4×15000B=100000B dollars. (4 attendants for each machine)

Canning cost=60000C+3×15000B=105000C dollars. (3 attendants for each machine)

Total cost=100000B+105000C.

Production per hour and constraints: (red) 150B+250C≥2000 cases; 250C≤1200 cases, 5C≤24 (yellow region).

Worker availability and constraints: (blue) 45≤4B+3C≤55 (green).

The feasibility region is in the yellow region, on or above red and blue lines and on or below the green line. We need to minimise total cost of 100000B+105000C. This appears to be the intersection of the red and blue lines. At this intersection B and C to have the smallest values.

150B+250C=2000, 45=4B+3C is the system of equations to be solved.

These equations can be reduced to:

3B/5+C=8, 15=4B/3+C, so 8-3B/5=15-4B/3.

Multiply through by 15:

120-9B=225-20B,

11B=105, B=105/11 and C=8-63/11=25/11.

We need to take these to the next highest integer, so B=10 and C=3. Note that (10,3) is in the feasibility region in the picture.

However, (9,3), near to the intersection of the blue and red lines, is also in the feasibility region (see picture) and incurs a lower cost, because B=9 is smaller than B=10.

The optimum cost is therefore $900000+$315000=$1,215,000, that is, 9 bottling and 3 canning machines.

CHECK

No more than 1200 soda can cases per hour: 250C=750<1200. OK.

At least 2000 cases/hr: 150B+250C=1350+750=2100>2000. OK.

Between 45 and 55 workers: 4B+3C=36+9=45. OK (minimum number of workers).

All constraints met.