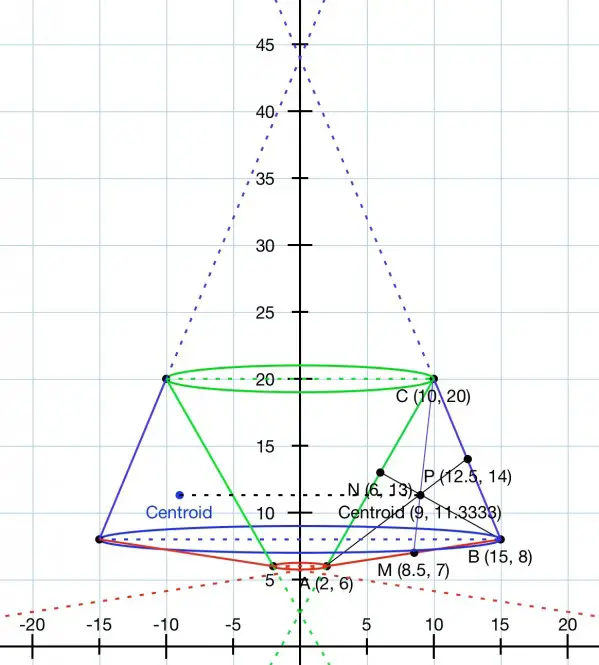
The centroid is the intersection of the medians.
The midpoints of the sides is located at the average of the coordinates of the endpoints.
Midpoint of AB=M(8.5,7), midpoint of AC=N(6,13), midpoint of BC=P(12.5,14).
We can find the intersection of two medians to find the centroid. First we need the equations of two medians:
Gradient of MC=(20-7)/(10-8.5)=13/1.5=26/3;
equation of MC: y=(26/3)(x-10)+20.
Gradient of PA=(14-6)/(12.5-2)=8/10.5=16/21;
equation of PA: y=(16/21)(x-2)+6.
So (26/3)(x-10)+20=(16/21)(x-2)+6.
Multiply through by 21: 182x-1820+420=16x-32+126.
(182-16)x=1820-420-32+126=1894, x=1494/166=9.
Therefore y=-26/3+20=34/3.
The centroid is (9,34/3).
When the triangle is rotated about the y-axis, the sides of the triangle form frustums as shown below.
We need to find a formula for the volume of a frustum, which is the difference in volumes of two cones, a smaller cone with dimensions r and h, and a larger cone with dimensions R and H, being the radius and height. Let the height of the frustum, d=H-h. Also, let p=r/R=h/H, because the two cones are similar figures.
V, volume of frustum=⅓πR²H-⅓πr²h=⅓πR²H(1-p³). But d=H-h=H(1-p).
V=⅓πR²d(1-p³)/(1-p)=⅓πR²d(1+p+p²)=⅓πR²d(1+(r/R)+(r/R)²).
The red and blue frustums are hollowed out by the green frustum, so we can work out all the frustum volumes and obtain the volume of the figure of revolution: blue+red-green=
⅓π[225×12(1+2/3+4/9)+225×2(1+2/15+4/225)-100×14(1+1/5+1/25)]=
1494π=4693.54 cubic units approx.