If the number of objects is x, 5423=-3.2x²+268.2x+257.
3.2x²-268.2x+5423-257=0, 3.2x²-268.2x+5166=0
Multiply through by 5: 16x²-1341x+25830=0.
Divide through by 16: x²-1341x/16+12915/8=0.
Halve the middle term and square it: (1341/32)².
Now we can complete the square: (x-1341/32)²-(1341/32)²+12915/8=0.
It happens that -(1341/32)²+12915/8=-(381/32)².
Therefore we have the difference of two squares: (x-1341/32)²-(381/32)²=0 which factorises:
(x-1341/32-381/32)(x-1341/32+381/32)=
(x-1722/32)(x-960/32)=(x-861/16)(x-30)=0.
Therefore $5423 profit is achievable with exactly 30 objects.
The other solution gives us 861/16=53.8125 objects, which is not a whole number. (53 objects raises a profit of $5482.80 and 54 objects a profit of $5408.60.)
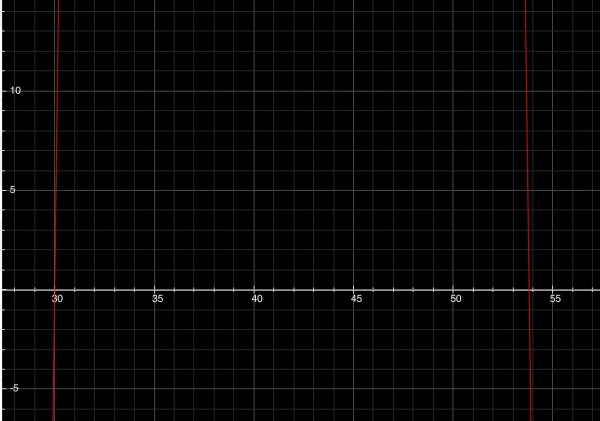
This graph of f(x)=5423 (red curve) shows the curve passing through x=30, and between 53 and 54, confirming the solution.