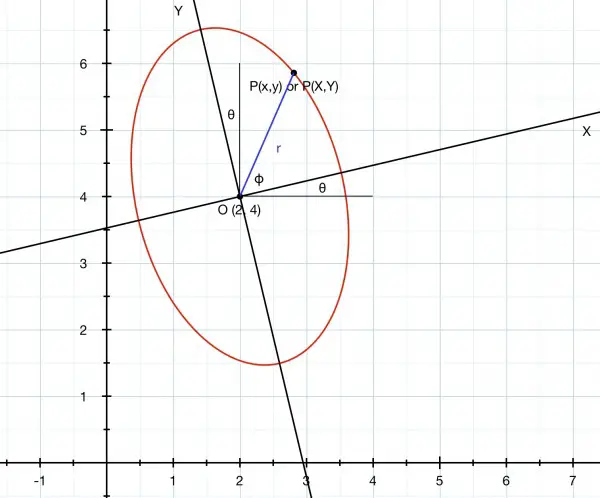
If X-Y is the Cartesian frame of reference for the curve which has its centre (origin) at O(h,k) wrt the x-y frame, then if P(X,Y)≡P(x,y), that is, P can be represented in either frame of reference, r²=OP²=X²+Y²=(x-h)²+(y-k)²=x²-2hx+h²+y²-2ky+k². We know that P must be on the curve 3x²+xy+y²-16x-10y+30=0. See picture.
Let θ=angle between the X-axis and the x-axis and ɸ=angle between OP and the X-axis.
X=rcosɸ, Y=rsinɸ, x-h=rcos(θ+ɸ), y-k=rsin(θ+ɸ).
x-h=rcosθcosɸ-rsinθsinɸ=Xcosθ-Ysinθ,
y-k=rsinθcosɸ+rcosθsinɸ=Xsinθ+Ycosθ.
The next step is to substitute for x and y to get an equation for X and Y. From this transformed equation we can find out which coefficients need to be zero so as to eliminate first degree terms.
To simplify writing, s=sinθ and c=cosθ.
x=h+Xc-Ys, y=k+Xs+Yc.
3x²=3h²+6h(Xc-Ys)+3(Xc-Ys)², y²=k²+2k(Xs+Yc)+(Xs+Yc)².
xy=hk+hXs+hYc+kXc+X²sc+XYc²-kYs-XYs²-Y²sc.
The XY term must be zero. If we look at what can produce XY, we see 3x² contains -6XYsc, y² contains 2XYsc and xy contains XY(c²-s²). Therefore, -6sc+2sc+c²-s²=0, c²-4sc-s²=0. Divide through by c²:
1-4t-t²=0 where t=s/c=tanθ. So t²+4t=1, t²+4t+4=5, (t+2)²=5, t=-2±√5.
The two angles for θ are 13.28° and 283.28°. These angles differ by 270° (3 right angles). This means that the X-axis is inclined to the x-axis by 13.28° or the Y-axis is inclined to the x-axis by 13.28°. This is the angle we’ll use to find h and k.
Therefore s=0.229753 and c=0.973249 approx.
To find h and k we look at the remaining coefficients. We are eliminating X and Y terms.
Start with X terms:
6hc+2ks+hs+kc-16c-10s=0; h(6c+s)+k(2s+c)=16c+10s; k=(16c+10s-h(6c+s))/(2s+c).
Y terms:
-6hs+2kc+hc-ks+16s-10c=0; h(-6s+c)+k(2c-s)=-16s+10c; k=(-16s+10c-h(-6s+c))/(2c-s).
We have sufficient to find h and k. Find h first:
(16c+10s-h(6c+s))/(2s+c)=(-16s+10c-h(-6s+c))/(2c-s). The only unknown is h.
(17.87-6.07h)/1.43=(6.06+0.41h)/1.72, 12.47-4.24h=3.52+0.24h, 8.94=4.47h, h=2 and k=4.
Please note that only 2 decimal places have been shown, but greater accuracy was obtained using a calculator.