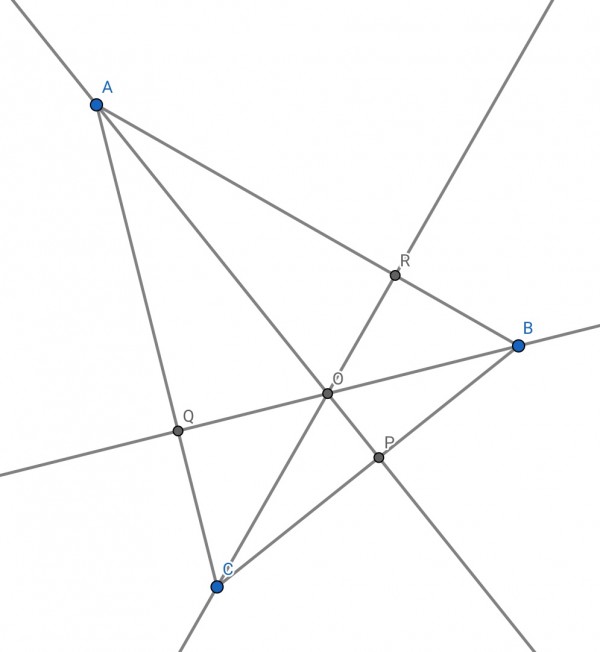
The orthocentre is point O in the picture. You can see that O divides the altitudes in different ratios.
So to find out where the intersection point is let the vertices be A(x₁,y₁), B(x₂,y₂), C(x₃,y₃).
Slope of QB=-1/(slope of AC)=-1/((y₃-y₁)/(x₃-x₁))=(x₁-x₃)/(y₃-y₁)=m₁,
Slope of PA=-1/(slope of AB)=-1/((y₂-y₁)/(x₂-x₁))=(x₁-x₂)/(y₂-y₁)=m₂.
The reason for introducing m₁ and m₂ is to simplify and clarify the calculations that follow.
The equation of the line including segment QB is y-y₂=m₁(x-x₂), that is, y=m₁(x-x₂)+y₂ because it passes through B(x₂,y₂). Similarly, the equation for PA is y=m₂(x-x₁)+y₁ because it passes through A(x₁,y₁).
By equating the two equations for y: m₁(x-x₂)+y₂=m₂(x-x₁)+y₁. So m₁x-m₁x₂+y₂=m₂x-m₂x₁+y₁. x(m₁-m₂)=m₁x₂-m₂x₁+y₁-y₂, and x=(m₁x₂-m₂x₁+y₁-y₂)/(m₁-m₂). Knowing x we can find y:
y=m₁(x-x₂)+y₂=Y. Let X=(m₁x₂-m₂x₁+y₁-y₂)/(m₁-m₂). Again, X and Y have been introduced to simplify the notation. The point O is (X,Y).
To find the ratio of the intersection and a particular altitude, for example, OQ/BQ, we need to find the lengths OQ and BQ. We need the coords of Q, which is the intersection of AC and BQ.
Equation of AC: y=(-1/m₁)(x-x₁)+y₁
Equation of BQ: y=m₁(x-x₂)+y₂
(-1/m₁)(x-x₁)+y₁=m₁(x-x₂)+y₂ can be solved for x, and then y can be found using either of the two equations.
Pythagoras’ Theorem is used to work out the lengths of OQ and BQ.
The ratios for the other two altitudes can be found similarly.
The best way to understand the process is to use actual coords of A, B and C.
An example follows.
A(-4,5), B(3,1), C(-2,-3).
Slope of AC=(-3-5)/(-2+4)=-8/2=-4. Slope of QB=¼.
Equation of AC: y-5=-4(x+4), y=-4x-16+5=-4x-11.
Equation of QB: y-1=¼(x-3), y=x/4-3/4+1=x/4+1/4.
Coords of Q: -4x-11=x/4+1/4, -16x-44=x+1, 17x=-45, x=-45/17; y=-4(-45/17)-11=180/17-11=-7/11. Q(-45/17,-7/11).
Slope of BC=(-3-1)/(-2-3)=-4/-5=⅘.
Equation of BC: y-1=⅘(x-3)=4x/5-12/5, y=4x/5-12/5+1=4x/5-7/5.
Equation of AP: y-5=(-5/4)(x+4)=-5x/4-5, y=-5x/4.
Coords of P: 4x/5-7/5=-5x/4, 16x-28=-25x, 41x=28, x=28/41; y=-(5/4)(28/41)=-35/41. P(28,41,-35/41).
Coords of O: x/4+1/4=-5x/4, 3x/2=-1/4, x=-(2/3)(1/4)=-1/6; y=-(5/4)(-1/6)=5/24. O(-1/6,5/24).
QB=√((3+45/17)²+(1+7/11)²); QO=√((-1/6+45/17)²+(5/24+7/11)²).
So QO/QB=√((-1/6+45/17)²+(5/24+7/11)²)/√((3+45/17)²+(1+7/11)²)=2.6203/5.8794=0.4457 approx.
Other ratios may be similarly calculated.