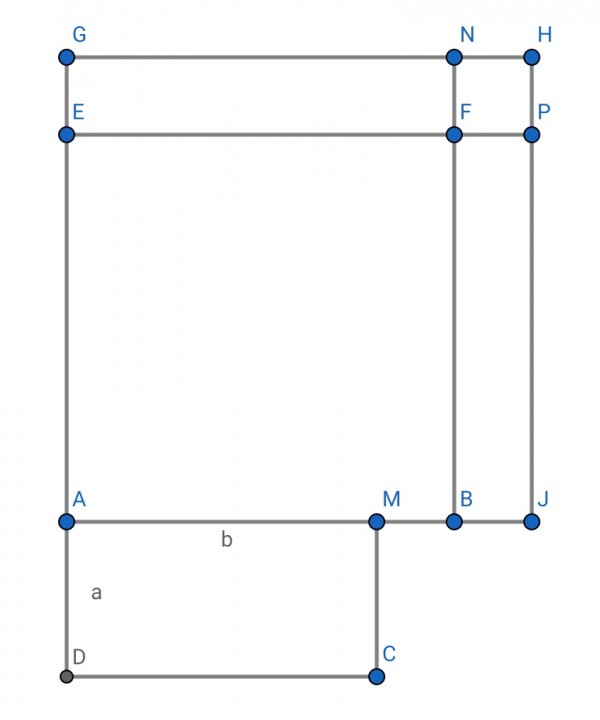
In the diagram there is a rectangle AMCD, with dimensions a and b, such that ab=c, the area. Above it is a square EFBA with side x, so the area of the square is x². The square is extended by increasing its side length by h=EG=BJ.
A larger square GHJA is produced, with side x+h. The increase in area can be found by summing the areas of its components: rectangles GNFE and FPJB and square NHPF. The respective dimensions of these are x and h, x and h, and side length h. The sum total of their areas are 2xh+h². The same result is obtained by subtracting the area of EFBA from GHJA. NHPF is small compared to the area of the long rectangles GNFE and FPJB.
If h is reduced, the difference between the areas of the two squares EFBA and GHJA. The area of NHPF is between 0 and some finite value h². If h is halved, (h→½h), for example, the area of NHPF is ¼h². The areas of GNFE and FPJB become xh/2, combined to make xh which is much larger than ¼h². So from the geometry, as h shrinks to zero, the areas of the rectangles are 2xh, which is dependent on x, which is unlimited in size. The derivative is 2xh/h=2x, that is, the rate of change of the area is 2x, dependent only on the side of the square.
Note that the constant area c=ab of rectangle AMCD is unaffected by these changes, so this rectangle can have any arbitrary size without affecting the derivative.
However, this only suggests that 2x is the derivative of x²+c. To start with the derivative 2x and work towards the primitive requires a different geometry:...
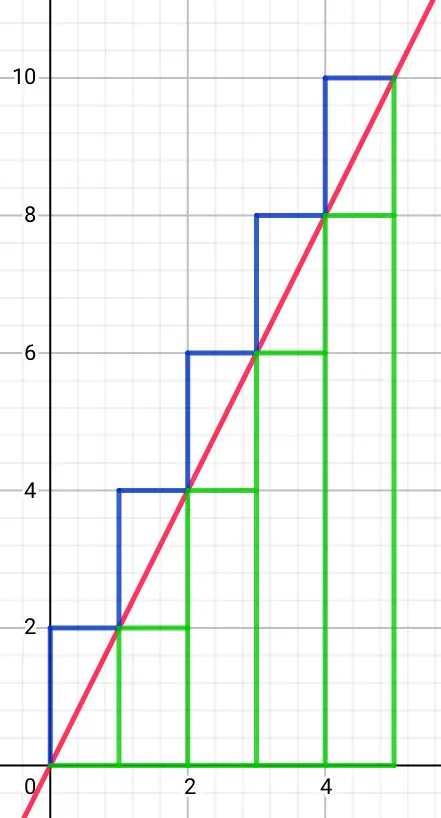
This time in the diagram above we start with the red line which is a graph of y=2x. The area between the line and the horizontal x-axis can be approximated to the sum of the areas of the rectangles drawn partly above the line or wholly below the line. The line is encapsulated between the two sets of rectangles. If the rectangles have a width h, the heights of the blue rectangles are 2h, 4h, 6h, ..., while the heights of the green rectangles are 0, 2h, 4h, .... if the horizontal limit is from 0 to an arbitrary value X. The height of the leftmost blue rectangle is 2h, so its area is 2h². The height of the first green rectangle is 0. The height of the second blue rectangle is 4h, area 4h²; the height of the second green rectangle is 2h, area 2h². If X/h=N, because the length X is divided into N segments of length h, then the sum of the rectangle areas is 2h²(1+2+3+...+N) (blue) and 2h²(0+1+2+...+N-1) (green). That is, 2h²N(N+1)/2=h²N(N+1) (blue) and h²N(N-1) (green). The area under the red line is between these two values, so if we replace N by X/h, we get h²(N²-N)<area<h²(N²+N), that is, h²(X²/h²-X/h)<area<h²(X²/h²+X/h). Expanding: X²-Xh<area<X²+Xh. We can see from this that as h gets smaller the area→X², which is also the triangular area between the red line and the x-axis. But we only took a definite area between 0 and X. If this constraint is removed and we take an indefinite area X² will be increased by an amount which we could call c. Hence the general (indefinite integral or anti-derivative) x²+c.