I finally figured it out. Here is the series up to x=100:
x: 0, 10, 20, 30, 40, 50, 58, 60, 70, 80, 90, 100
f(x): 1, 6, 12, 15, 69, 1025, 9415, 14456.11302, 81768.79114, 302500.1645, 871801.4936, 2127107.734
Apologies for poor resolution, but the explanation tomorrow will provide the necessary details.
f(x)=1-1394.55217(x/10)+3216.99301(x/10)²-2670.285319(x/10)³
+1025.305009(x/10)⁴-185.2190212(x/10)⁵+12.75849031(x/10)⁶.
METHOD
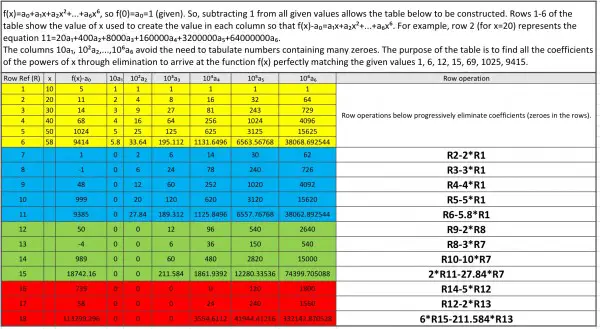
Let f(x)=a₀+a₁x+a₂x²+...+a₆x⁶, a power series in x. When x=0, f(0)=a₀=1 (the first y value given). So, subtracting a₀=1 from the remaining y values gives the values in column f(x)-a₀ in rows 1-6 of the table (yellow section). Each row represents an equation. For example, row 2 (for x=20) represents:
11=20a₁+400a₂+8000a₃+160000a₄+3200000a₅+64000000a₆.
The columns 10a₁, 10²a₂,...,10⁶a₆ avoid the need to tabulate numbers containing many zeroes. The purpose of the table is to find all the “a” coefficients of the powers of x through elimination to arrive at the function f(x) matching as closely as possible the given values of y: 1, 6, 12, 15, 69, 1025, 9415.
The table is divided into coloured sections with decreasing numbers of rows until we have sufficient information to deduce all the coefficient values. All the values in the table “equations” are shown to 100% accuracy. It is only when we take the values in the red section and use them to find the values of the coefficients that the accuracy is reduced to ten significant figures.
In the last column of the table we have a description of the row required to generate zeroes in the table equations. The Row Ref (R) column identifies the rows, and the Row operation column applies to rows 7-18. For example, the row operation for row 10 says “R5-5*R1”, which means subtract 5 times the values in row 1 from those in row 5 (columns f(x)-a₀ to 10⁶a₆). The aim is to generate zeroes in at least one column, meaning that we have eliminated a coefficient.
Each coloured section shows the progress of elimination starting with a₁ in the blue section up to a₃ in the red section. The values involving x=58 and the resulting row operations get increasingly more fiddly, with many decimal places, but this is to maintain 100% accuracy within the table itself.
The red section contains sufficient information to find the coefficients a₄, a₅ and a₆ as given by the equations in rows 16-18:
(16) 120a₅×10⁵+1800a₆×10⁶=739
(17) 24a₄×10⁴+240a₅×10⁵+1560a₆×10⁶=58
(18) 3554.6112a₄×10⁴+41944.41216a₅×10⁵+332142.870528a₆×10⁶=113299.296.
Clearly, the calculations are becoming tedious!
In (16) we can find a₅ in terms of a₆, then, by substituting for a₆ in (17) we can find a₄ in terms of a₆. Substituting for a₅ and a₄ in (18) we get an equation in coefficient a₆ alone and so we can find its value, but, for convenience we use a₆×10⁶ to avoid awkward decimal fractions with many leading zeroes:
a₆×10⁶=12.758490305, accurate to 9 decimal places. From this we can derive a₅ and a₄. Progressively, starting with any equation in the green section we can find a₃. The blue section equations are used for finding a₂ and row 1 (conveniently) gives us a₁.
So we have f(x) by plugging in all the coefficients including a₀=1.
The final form of f(x) uses a power series in x/10 instead of x, because it’s easier to read the coefficients that way.