Question

Sketch a graph of a function g satisfying the following conditions: g is periodic with a period T=2, the domain is D(g) = all real numbers g(x)= 1-x for x ϵ [0,2). Is your g continuous?

Answer 1

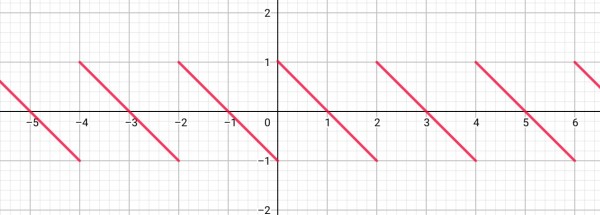
g is not continuous. g(x+2)=g(x), so g(2)=g(0) but g(0)=1, so g(2)=1.

The left limit for x→2 is 1-2=-1 and the right limit is 1. These limits are not the same so there is discontinuity at x=2. This discontinuity is repeated indefinitely for the whole of g(x). Note that the lines are closed at their upper ends but open at their lower ends, because g(x)=1-x for x∈[0,2), which is open-ended at its high limit.