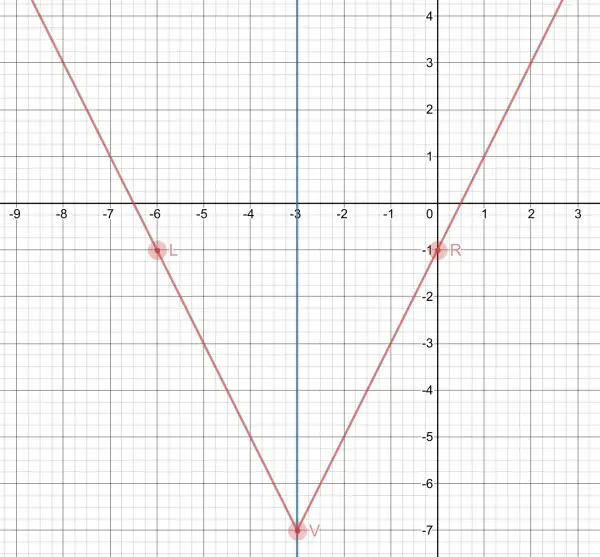
|x+3| is always positive so its lowest value is zero, which is x+3=0, x=-3.
The lowest value for y must be when x=-3, and the lowest point is the vertex.
So since |x+3|=0, y=-7, so mark the point V(-3,-7) on your graph. Another point which is easy to plot is when x=0, y=2×3-7=-1, giving you R(0,-1), The y-intercept. You do need another point to draw the V-shaped graph, or you can use the axis of symmetry which is the vertical line x=-3 as a mirror to reflect the point (0,-1). To get from the vertex at (-3,-7) to (0,-1) you have to move 3 units to the right and 6 units up, so its reflection is 3 units to the left of the vertex and 6 units up giving you L(-6,-1) (the y coordinate doesn’t change).
Draw a ray starting at the vertex to L(-6,-1) (the left arm of the V) and another ray from the vertex to R(0,-1) (the right arm of the V).
You can see that L and R are reflections of one another in the “mirror” x=-3, the blue vertical line.