Find the sum of the first six terms of the following A.P. Find the formula for Sn and graph the Sn of the first two series.

Question

<!--[if !supportLists]-->1.               <!--[endif]-->8, 6, 4, …

 

<!--[if !supportLists]-->_2.                                    <!--[endif]-->4, 2, 0, …

 

<!--[if !supportLists]-->3.               <!--[endif]-->-4, -2, 0, …

 

<!--[if !supportLists]-->4.               <!--[endif]-->22, 25, 28, …

 

<!--[if !supportLists]-->5.               <!--[endif]-->18, 14, 10, …

 

 

 

Answer 1

Here are your answers.

1 and 2 )  https://ibb.co/R7NS1vv
3 and 4 )  https://ibb.co/3zkZxTT
5) https://ibb.co/S0CFrjx

Graph of 1) https://ibb.co/bmCVpY5
Graph of 2)  https://ibb.co/2KBLC5J

Comments

Correction,

4) Last line, (41*6 + 3* 36)/2 = 177

5) Last line, 20*6 - 2*36 = 48

Answer 2

In the following d is the common difference.

1) 8, 6, 4, 2, 0, -2; S₆=18 (add the terms); d=-2

2) 4, 2, 0, -2, -4, -6; S₆=-6; d=-2

3) -4, -2, 0, 2, 4, 6; S₆=6; d=2

4) 22, 25, 28, 31, 34, 37; S₆=(22+37)+(25+34)+(28+31)=3×59=177; d=3

5) 18, 14, 10, 6, 2, -2; S₆=48; d=-4

Call the first term a, so T₁=a and d=common difference, so T₂=a+d and T_n=a+(n-1)d.

Now look at (4) and how the sum was formed by taking pairs of terms. The sum of the first and last terms help us to find a formula for S_n.

The sum of each pair is a + (a+(n-1)d)=2a+(n-1)d. The number of terms is halved=n/2 and this is the multiplier of the pair-sum, hence S_n=(n/2)(2a+(n-1)d) or n(2a+(n-1)d)/2. If n is odd, this formula still works because the middle term is added to itself (doubled) then halved.

Let's see what happens when we use the formula to answer the questions:

1) a=8, d=-2, n=6; S₆=6(16-10)/2=18; 2) a=4, d=-2, n=6; S₆=6(8-10)/2=-6

3) a=-4, d=2, n=6; S₆=6(-8+10)/2=6; 4) a=22, d=3, n=6; S₆=6(44+15)/2=177

5) a=18, d=-4, n=6; S₆=6(36-20)/2=48.

To draw graphs we need to find an equation for each of (1) and (2).

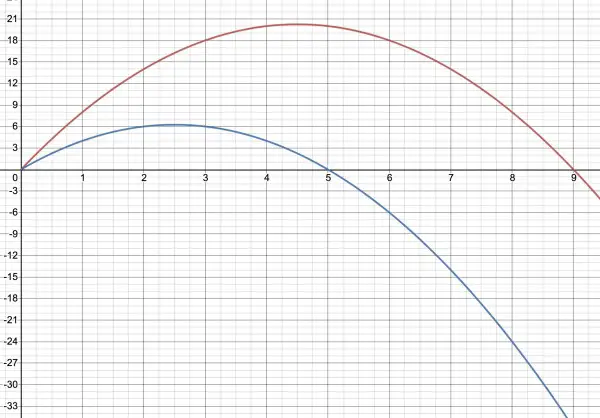
1) S(n)=n(16-2(n-1))/2=n(8-n+1)=9n-n² (red)

2) S(n)=n(8-2(n-1))/2=n(4-n+1)=5n-n² (blue)

Only integer values >0 are relevant on these graphs. Note S=18 (red) and -6 (blue) when n=6. Note also that S=0 when n=9 (red) or 5 (blue). So the graphs are useful for a better overview.