Solve the linear algebra

Question

please solve this 

Answer 1

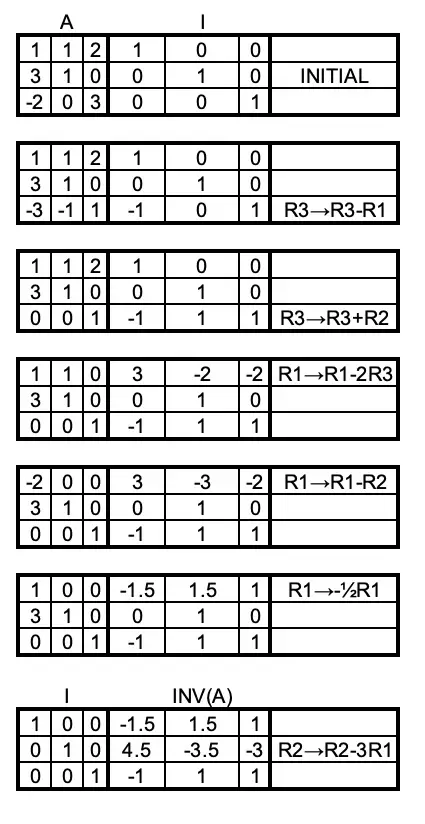
Now (I) The technique is based on expanding the matrix to contain the given matrix alongside the identity matrix. Using row operations, the aim is to get the identity matrix to change places with the inverse. 

IIa) 2A+B=

⎡ -2 4 ⎤

⎣ 18 8 ⎦+

⎡ 3 -2 ⎤

⎣ 4  5 ⎦=

⎡  1     2 ⎤

⎣ 22  13 ⎦

IIb) AB=

⎡ -1 2 ⎤⎡ 3 -2 ⎤

⎣ 9  4 ⎦⎣ 4  5 ⎦=

⎡  -3+8       2+10 ⎤

⎣ 27+16  -18+20 ⎦=

⎡  5  12 ⎤

⎣ 43   2 ⎦

III) 

Make a matrix of the coefficients then find its determinant Δ=

4((2)(-2)-(3)(-2))+((2)(-2)-(5)(3))-((2)(-2)-(5)(2))=

4(-4+6)+(-4-15)-(-4-10)=8-19+14=3.

Now make 3 matrices, one for each variable, replacing the variable column with the column of constants. Calculate the determinants of these matrices to get Δ₁, Δ₂, Δ₃. Divide each of these by Δ (=3) to get the solution for each variable.

For Δ₁, Δ₂, Δ₃ I get 3, 3, 6 respectively, so dividing each by 3 we arrive at x₁=x₂=1, x₃=2.

Check: 4-1-2=1✔️; 2+2+6=10✔️; 5-2-4=-1✔️

IV) If a, b and c are scalars then we can write the following system of equations:

a+c=2

a+b=5

b+c=3

This is easy to solve without using matrices:

Add the first two equations together: 2a+b+c=7, 2a+3=7 (because b+c=3), a=2⇒c=0, b=3.

v=2u₁+3u₂. This is the only solution. <2,5,3>=<2,2,0>+<0,3,3>

Answer complete.