Question

Find the area of the “triangular” region in the first quadrant that is bounded above by the curve y =e^2x below by the curve y = e^x, and on the right by the line x = ln 3.

Answer 1

A picture helps:

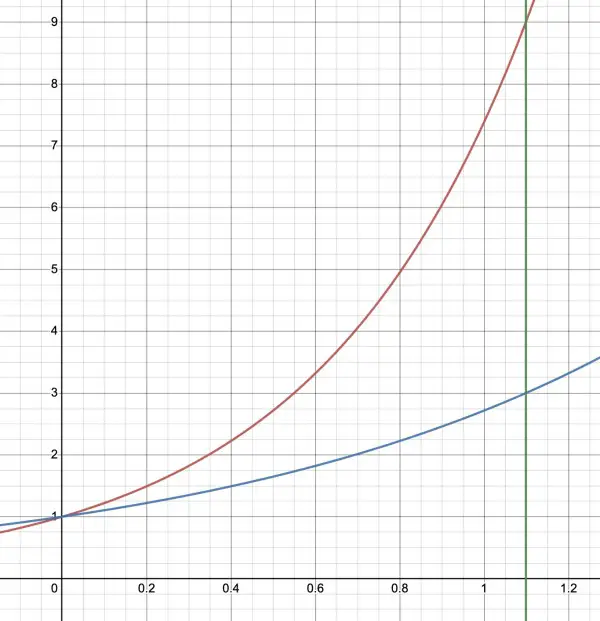
y=e^2x is in red, y=e^x is in blue, and the boundary line x=ln(3) is in green. Note that 2x=2ln(3)=ln(9).

The relevant area is easy to see. Imagine the area divided into thin vertical rectangles of width dx, height e^2x-e^x, so the sum of the areas of these rectangles is e^2x-e^x and is the integral:

∫(e^2x-e^x)dx, between the limits 0 and ln(3).

This comes to ½e^2x-e^x=½e^ln(9)-e^ln(3)-(½-1)=9/2-3+½=2. So the area is 2 sq units.