5x+2y=7, -2x+6y=9.
From the first equation 2y=7-5x. The second equation contains 6y so we can find out what 6y is by multiplying 2y=7-5x by 3 on both sides: 6y=21-15x.
Now we can replace 6y in the second equation with 21-15x:
-2x+21-15x=9 and then solve for x:
21-17x=9, so 21-9=17x, 12=17x so 17x=12 and, dividing both sides by 17 we get x=12/17.
To find y we substitute this value of x in either of the two given equations.
5(12/17)+2y=7 is the first equation, with substitution. 60/17+2y=7, so 2y=7-60/17=(119-60)/17=59/17, making y=59/34 (halve each side).
We need y to the nearest tenth so 59/34=1+25/34=1.7 approximately. (One way to get the decimal in this case is to multiply top and bottom by 3: 75/102. This is almost the same as 75/100=0.75, but it's a bit smaller because 102 is bigger than 100 so 25/34 is less than 0.75. We only need one place of decimals (the nearest tenth) which is 0.7. Add on 1 and we get 1.7.)
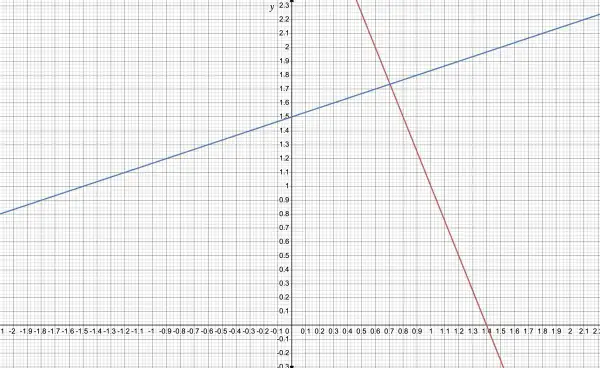
A graph of the two lines should produce the same result by looking at where the lines intersect. The red line is 5x+2y=7 and the blue line -2x+6y=9. The scale of the graph shows the y coordinate of the intersection to be about 1.7 (and the x-coordinate about 0.7).
Picture courtesy of Desmos.com/calculator