a) Whatever a is, the graph passes through the origin (which is also the inflexion point) when b=0. The graph is almost horizontal close to the origin. If a>0, the graph gets narrower as a increases. When x>0 the graph rises slowly (positively) until x=1, then it rises more steeply for x>1. When x<0, the graph becomes negative when x>-1 and falls slowly (negatively) until x=-1, then it falls more steeply for x<-1. If a<0 the graph has the same shape as the corresponding positive values for a, but it’s reflected in the x-axis. Because of symmetry, this looks the same as a reflection in the y-axis.
b) If a and b are both positive, the shape is the same as in (a) but the point of inflexion shifts up the y-axis by the value b. If they’re both negative the graph is reflected and moves down with the point of inflexion at (0,b) below the origin. If a>0 and b<0 the shape is as in (a) but the point of inflexion is below the origin. If a<0 and b>0 the shape is as in (a) where reflection occurs but the point of inflexion is above the origin.
c) To find the gradient we differentiate y to get dy/dx=3ax². So when x=p, the gradient is 3ap². The tangent line at this point is y=3ap²x+c and to find c we plug in the tangent point (p,ap³+b):
c=ap³+b-3ap³=b-2ap³. Therefore the tangent line is y=3ap²x+b-2ap³.
The tangent line meets the curve when 3ap²x+b-2ap³=ax³+b, that is, x³-3p²x+2p³=0. We know a factor of this is x-p because of the tangent point which lies on the line, so we can divide x³-3p²x+2p³ by x-p to give us x²+px-2p²=(x+2p)(x-p), so x=-2p is the only intersection point. [x³-3p²x+2p³=0=(x-p)²(x+2p).] At the point of inflexion p=0 so this is the only tangent which does not intersect the curve, and all other points intersect at one point only, x=-2p.
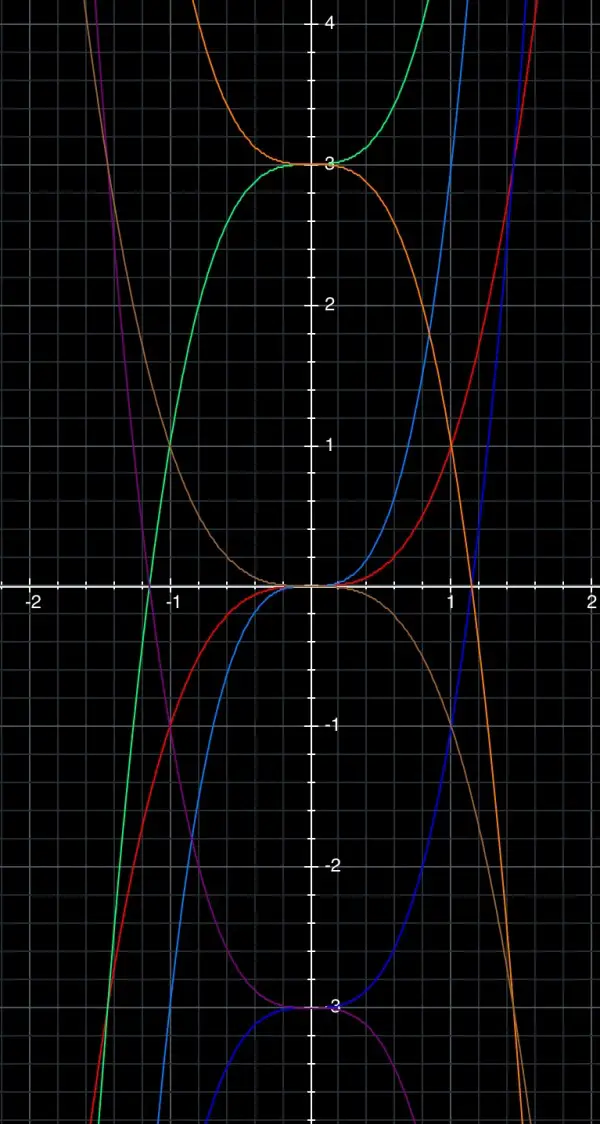
RED b=0 a>0, BROWN b=0 a<0, LIGHT BLUE b=0 and a>0 but bigger then a for the red curve.
GREEN a and b both positive, PURPLE a and b both negative.
DARK BLUE a>0 b<0, ORANGE a<0 b>0.