Write and graph a system of inequalities that can be used to find the amounts of each salt solution needed.

Question

a chemist wants to mix a new solution with at least 18% pure salt. the chemist has two solution with 9%pure salt and 24% pure salt and wants to make at most 250ml of the new solution. Write and graph a system of inequalities that can be used to find the amounts of each salt solution needed.

Answer 1

If a=volume of 9% solution and b=volume of 24% solution:

a+b≤250mL total volume.

Amounts of pure salt in ingredients: 0.09a and 0.24b.

Amount of pure salt in mixture: 0.18(a+b).

0.09a+0.24b≥0.18×250, 0.09a+0.24b≥45.

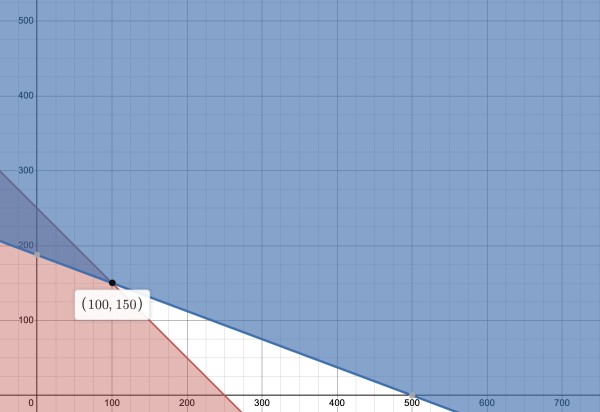
a is the horizontal axis and b the vertical axis.

The graph shows a+b≤250 as the red shaded region and 0.09a+0.24b≥45 as the blue shaded region. Note that a, b≥0.

The boundaries are represented by the vertices of the triangular region: (0,187.5), (100,150), (0,250). These represent (a,b) values.

The point (100,150) where the lines intersect represents optimal values: a=100mL, b=150mL.

100mL of 9% solution=9mL of pure salt; 150mL of 24% solution=36mL of pure salt. Total amount of pure salt in mixture=45mL, which is 45/250=18%.

The two regions overlap as shown, and it is the triangular region which represents all solutions to the inequalities.