The triangles are not congruent. Congruent triangles have matching angles and sides.
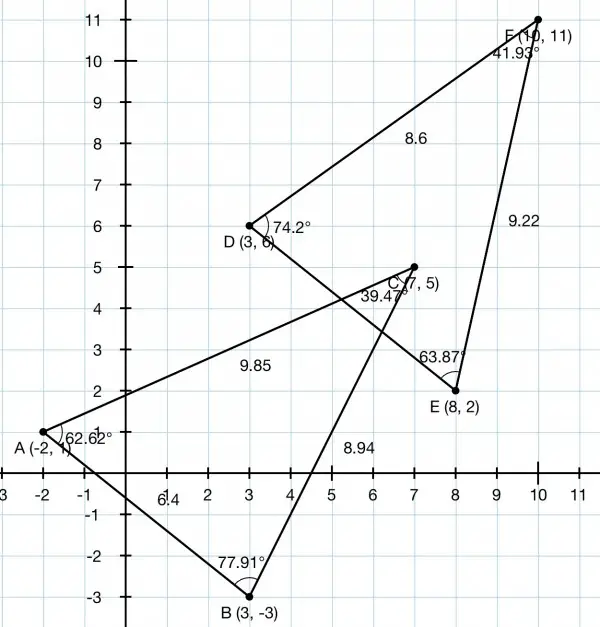
To work out the angles we can work out their tangents by taking the difference of the y values and dividing by the difference of the x values. These will give us external angles from which we calculate the internal angles.
Left external angle of B is tan B(L)=|1-(-3)|/|3-(-2)|=4/5. Right external angle B is tan B(R)=|5-(-3)|/|7-3|=8/4=2.
These angles are 38.66 and 63.43. So B=180-(38.66+63.43)=77.91.
All the angles of both triangles can be found this way and are shown in the picture. You can also count the squares to work out the tangents of the external angles. The y values are the numbers of squares vertically between two points and the x values are the numbers of squares horizontally between two points. Since none of the angles match the triangles can be neither similar nor congruent. Had they been identical, it would only require the length of two corresponding sides to be the same to prove congruency.
Interestingly, though, AB and DE are parallel and have the same length (by Pythagoras, √(4^2+5^2)=√41=6.4 approx), but the other sides are not parallel and differ in length (parallel lines have the same slope or tangent, which is 4/5 here). For example, EF has a slope of 9/2=4.5 while BC has a slope of 8/4=2.
So AB=DE but AC≠DF and AC≠EF (although they look very similar), and the triangles are not therefore congruent. The angles B and D also look to be the same, but calculations show they're not.