c(x)=(3x2-24x+48)/(x3-16x)=
3(x2-8x+16)/(x(x-4)(x+4))=
3(x-4)2/(x(x-4)(x+4))=3(x-4)/(x(x+4)) provided x≠4.
The denominator determines the vertical asymptotes (VAs) at x=0 and x=-4.
When x is very large and positive c(x)→3/x→0+ (approaches the x-axis from above); when x is very large and negative c(x)→3/x→0- (approaches the x-axis from below).
c(x) crosses the x-axis (x-intercept) when x=4, but this intersection point is in fact a hole (discontinuity), because when dividing numerator and denominator by the factor x-4 it is assumed that x≠4, which would cause zero divided by zero which, in theory, cannot be determined. So this part of the curve is effectively severed (split into two parts) by the hole.
The curve consists of three main parts:
(i) x<-4 has a horizontal asymptote (HA) at c(x)=0 (the x-axis), and is enclosed by the HA and VA=x=-4 (left on the graph);
(ii) -4<x<0 sits between the VAs (a U-shaped curve with its vertex some units above the x-axis), and is enclosed by the two VAs (central on the graph);
(iii) 0<x<4 sits between VA=x=0 and the hole, and x>4 sits between the hole and approaches the HA=x-axis (c(x)=0) (right on the graph).
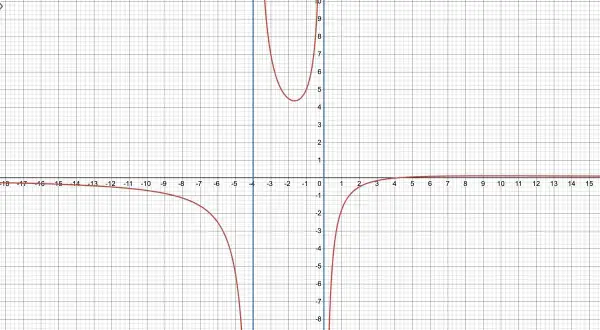
The VAs are shown in blue and the c(x) is shown in red. The HA is the x-axis. The hole is at (4,0).