Help finding the absolute and local maximum and minimum values of f?

Question

Use your sketch to find the absolute and local maximum and minimum values of f. (If there is not one, enter NONE.)

f(x) = 2 + (x + 1)²
-2 ≤ x < 7

Answer 1

Sketch the graph of f by hand and use your sketch to find the absolute and local maximum and minimum values of f. (If an answer does not exist, enter DNE.)

f(x) = 

3 − x		if 0 ≤ x < 5
4x − 20		if 5 ≤ x ≤ 7

 

Answer 2

f(x)=2+(x+1)² for -2≤x<7.

f(-2)=2+1=3; f(7)=2+64=66.

f'(x)=2x+2; when f'(-1)=0, which is the absolute minimum point (-1,2), the vertex of the parabola.

x=-1 lies between -2 and 7, so the absolute minimum is smaller than f(-2). The local maximum is f(7)<66, because the given interval does not include f(7), so the local maximum is NONE, although it approaches 66.

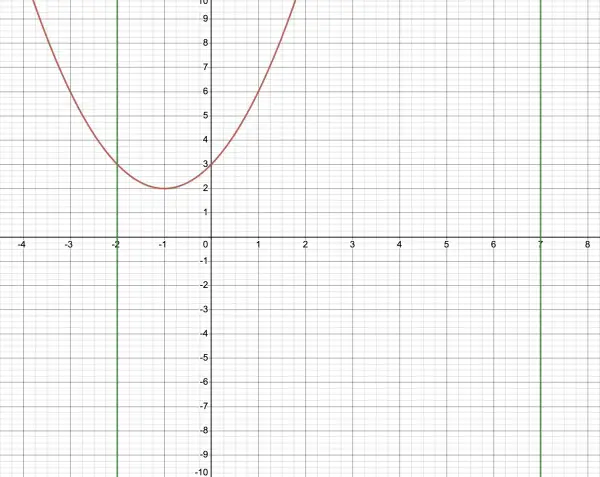
The green vertical lines mark the given interval.