Question

 

In triangle ABC, E is the mid point of median AD.

Show that ar(BDE)=1/4 ar(ABC).

Answer 1

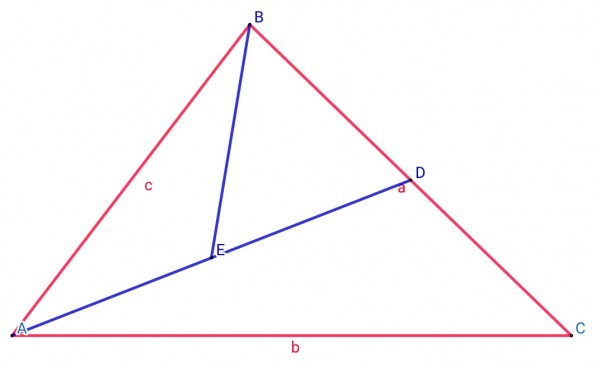
Area ABC=½absinC (two sides and the included angle).

Area BDE=½BD.DEsinADB=¼a×DEsinADB.

Note that sinADB=sinADC, because ∠ADB and ∠ADC are supplementary.

BD=½BC=½a because D is the midpoint of BC (AD is a median). Also AD=2DE because E is the midpoint of the median AD.

AD/sinC=b/sinADC (Sine Rule)=b/sinADB,

2DE/sinC=b/sinADB, sinADB=bsinC/(2DE).

Area BDE=¼a×DE(bsinC/(2DE))=⅛absinC=¼(½absinC)=¼(area ABC).