rational function problems

Question

F(x)=x^2+14x+24/x^2(x+5)

giving the zeros, midpoints, and the y-intercept

Answer 1

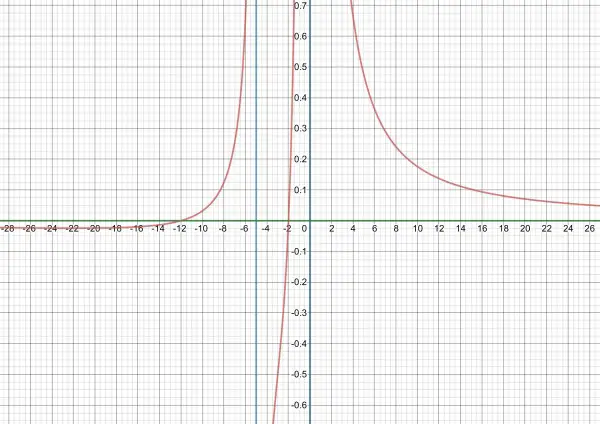
The numerator x²+14x+24=(x+12)(x+2) gives the x-intercepts (when y=0) x=-2, -12. 

There can be no y-intercepts because, when x=0, the function is undefined. 

There can be no midpoints because there are no finite segments defining endpoints. The midpoint of the x-intercepts is x=(-2-12)/2=-7.

The vertical asymptotes (blue) are when x²(x+5)=0, that is, x=0 (y-axis) and x=-5.

The horizontal asymptote (green) is when x is very large and the function reduces to y=1/x which approaches zero, so the horizontal asymptote is when y=0 (x-axis).