In all spherical triangles sin(a)/sin(A)=sin(b)/sin(B)=sin(c)/sin(C).
In a right spherical triangle where C=90°, this becomes sin(a)/sin(A)=sin(b)/sin(B)=sin(c).
But using the given info sin(a)/sin(A)=1.137 approx while sin(b)/sin(B)=0.654 approx. Clearly these are different so the triangle as described cannot exist.
Napier's Circle shows how to derive the ten Napier Rules:
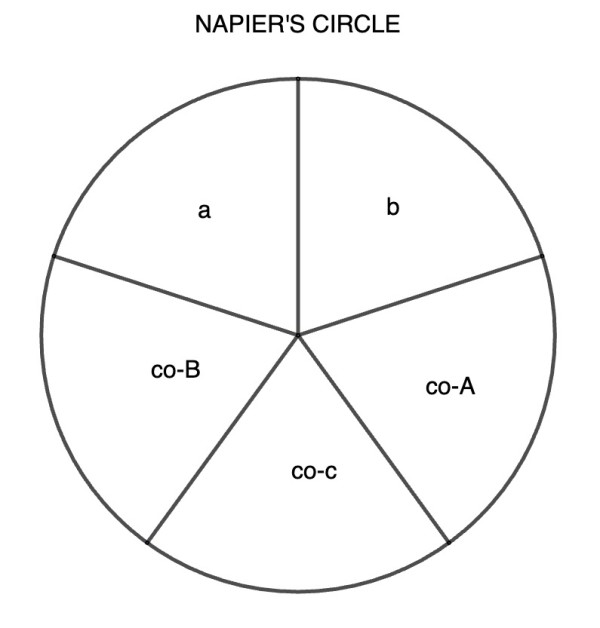
sin(middle)=cos(opposite1)cos(opposite2); sin(middle)=tan(adjacent1)tan(adjacent2).
Each middle segment of Napier's Circle has a segment on either side of it (adjacents 1 and 2), and two opposite segments (opposites 1 and 2). "co-" means complement, meaning that the trig function is reversed (cosine becomes sine and tangent becomes cotangent). Therefore if co- is the prefix (co-A, co-B, co-c) cos(co-A), for example, would become sin(A). Care has to be taken when finding arc lengths (also represented by an angle which subtends the arc (a spherical side of the triangle) in a unit circle) when the angle exceeds 90°, that is, an obtuse angle. An example of a pair of equations would be:
sin(a)=cos(co-c)cos(co-A)=sin(c)sin(A); sin(a)=tan(co-B)tan(b)=cot(B)tan(b). From the first equation sin(c)=sin(a)/sin(A)=1.137 (see earlier). Since sine cannot exceed 1, this shows that the given info does not describe a true spherical triangle. This equation also follows from the Sine Rule.
However, if (1) and (2) are separate questions, then we can use (2):
sin(b)/sin(B)=sin(c)=0.654465, c=40.88°, or 40°53'.
But we have angles greater than 90° so we need the supplementary angle 139°7'.
This still leaves (1) without a solution, because it violates the Sine Rule.