This looks like the equation of a hyperbola. To express it in standard form:
(x-x₀)²/a²-(y-y₀)²/b²=±1 (-1 means a hyperbola with vertical foci, 1 means a hyperbola with horizontal foci), where (x₀,y₀) is the centre, we need to complete the squares:
[y²-4y+4-4]-4[x²+2x+1-1]-4=0,
(y-2)²-4-4(x+1)²+4-4=0,
(y-2)²-4(x+1)²=4,
(x+1)²-(y-2)²/4=-1, from which the centre is (-1,2).
The foci (and hence the vertices) are vertically arranged.
When x=-1, y-2=±2, so (-1,4) and (-1,0) are the vertices.
The semiaxes are given by a and b in the standard form, and a=1 and b=2. The vertical transverse axis (y axis direction) is denoted by b, and its length is 2b=4. The conjugate axis has length 2a=2. The transverse axis is also the distance between the vertices=4 (difference of y coords).
The asymptotes are given by 4(x+1)²=(y-2)², that is 2x+2=y-2 and 2x+2=2-y. That is: y=2x+4 and y=-2x.
Focal distance=√(a²+b²)=√5.
We need to add and subtract the focal distance to the y coord of the centre to get the foci: (-1,2+√5) and (-1,2-√5).
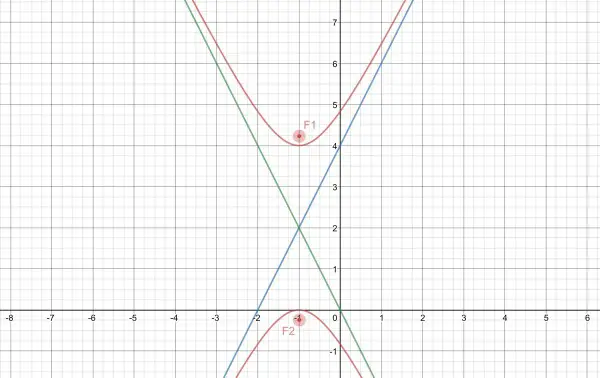
The asymptotes intersect at the centre (-1,2).
The directrices are at y=1 and y=3.