x^2+2x+4y-15=0 is the same as x^2+2x+1-16+4y=0.
So (x+1)^2=16-4y and 4(y-4)=-(x+1)^2. This is in standard parabola form (4f(y-k)=(x-h)^2 where (h,k) is the vertex and |f| is the focal length) with vertex at (-1,4). The parabola is inverted with axis x=-1 on which lies the focus, which is the same distance from the vertex as the directrix. The focus is on the inside of the curve while the directrix line is outside the curve and perpendicular to the parabola's axis. The latus rectum (the chord of the parabola) is parallel to the directrix and passes through the focus.
The focal length in this case is 1 and because it lies within the inverted curve its coord of the focus is (-1,3). The directrix line is above the curve at y=5. The latus rectum is at y=3 with endpoints where this line intersects the curve: -4=-(x+1)^2, x+1=±2 so the endpoints have x-coords ±2-1=1 and -3: (1,3) and (-3,3).
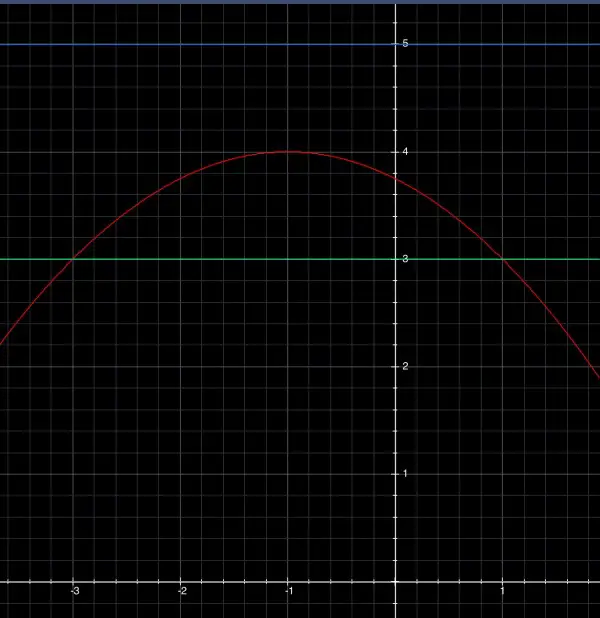
The parabola is the red curve and the blue line is the directrix line. The green line spanning the parabola is the chord (latus rectum) but is shown extended beyond the curve.