Question

Graph the parabola. Find the vertext, focus, directix and the endpoints of the latus rectum.

4y^2+2x=0

Answer 1

4y²+2x=0,

2x=-4y²,

x=-2y² is a "sideways" parabola with vertex at (0,0), axis of symmetry being the x-axis (y=0) containing the focus. 4fx=-y² where f is the focal length, so 4f=½, f=⅛. The focus is therefore at (-⅛,0).

The LR is perpendicular to the axis of symmetry and its endpoints have the same x coordinates as the focus, x=-⅛. Therefore we have -⅛=-2y², y²=1/16, y=±¼. The endpoints are (-⅛,¼) and (-⅛,-¼).

The directrix is a focal length to the right of the vertex, x=⅛.

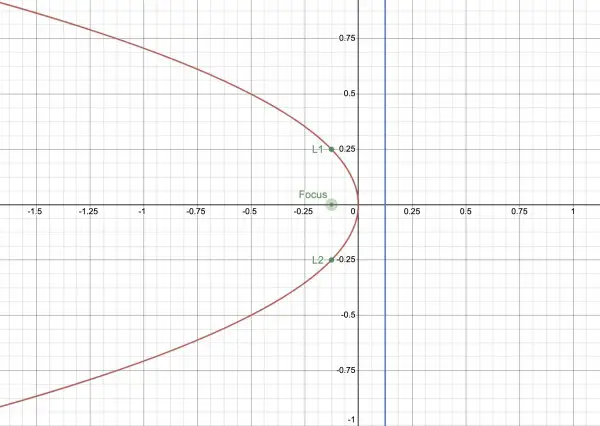
L1 and L2 are the endpoints of the LR. The blue line is the directrix. The focus is shown, and the vertex is the origin.