The focus lies on the axis of symmetry and the horizontal directrix line y=-6 is perpendicular to this axis. Therefore the axis of symmetry is vertical and because the x coord of the focus is 0, the axis of symmetry is the line x=0 (y axis). The vertex also lies on the axis of symmetry and midway between the focus and directrix line. The y coord of the vertex is halfway between y=-6 and y=6, so the vertex is at the origin (0,0). Therefore y=ax² where a is a constant to be found, is the general equation of this parabola. For all parabolas a=1/4f where f is the distance between the focus and the vertex (6,0)-(0,0)=6 along the y-axis. So a=1/24 and y=x²/24.
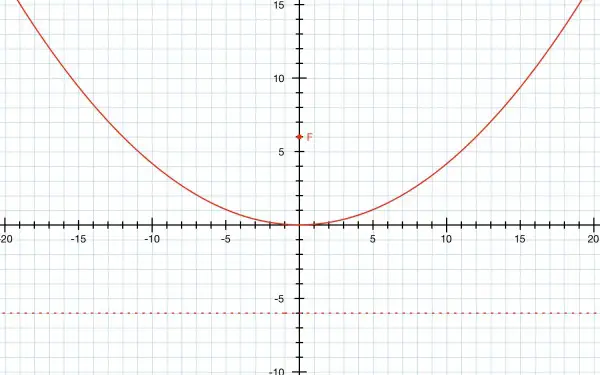
F is the focus and the dotted line is the directrix.