The slant length L, the vertical height h, the base radius r are related by Pythagoras: L^2=h^2+r^2. This formula means that, given any two of L, h, r, the third one can be found.
Cone volume=πr^2h/3=πr^2√(L^2-r^2)/3.
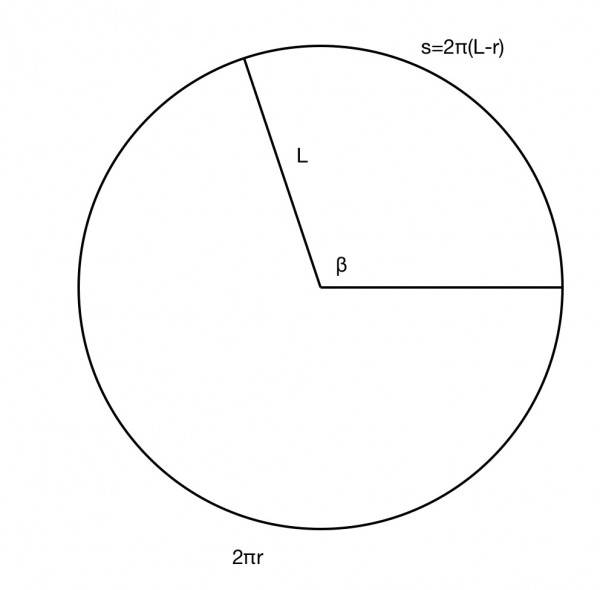
The picture shows a major sector of a circle that forms the surface area of a cone. The radius of the circle is the slant length L. The cone is formed by joining the arms of the sector. The arc of the sector forms the circular base of the cone, so the arc length is 2πr. The minor sector has an arc length s. Its area is represnted by A. The ratio of the minor sector area to the area of the large circle is the same as the ratio of the sector angle β to 2π:
A/(πL^2)=β/2π from which A=βL^2/2. But s=Lβ=2π(L-r), from which β=2π(L-r)/L. Therefore A=2π(L-r)/L.L^2/2=πL(L-r). The surface area of the cone itself is πL^2-A=πL^2-πL^2+πLr=πLr. However, this excludes the area of the base which is πr^2 and the total surface area is πLr+πr^2=πr(L+r).
These formulae show how the slant length comes into calculations of volume and surface area of a cone.