x^2-6x-y-3=0

Question

identify conic, then complete square to write conic in standard form

Answer 1

x²-6x-y-3=0,

y=x²-6x-3,

y=x²-6x+9-12,

y=(x-3)²-12 identifies a parabola with vertex at (3,-12). Focus is at (3,-11.75) and directrix line is y=-12.25.

The standard form is y+12=(x-3)² from general form y-k=a(x-h)², where (h,k) is the vertex, so a=1, h=3, k=-12.

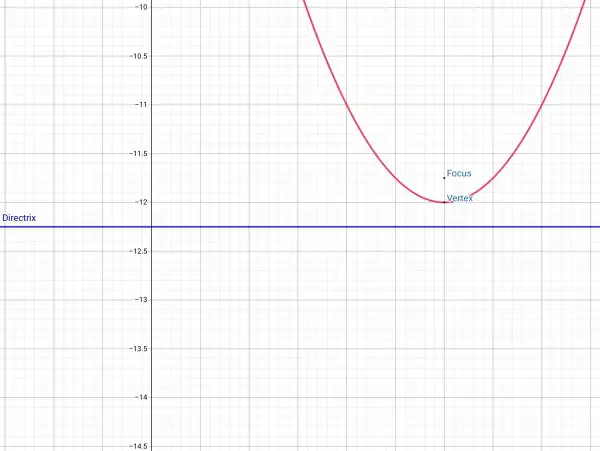
The focus is a/4 units above the vertex while the directrix line is a/4 units below the vertex.