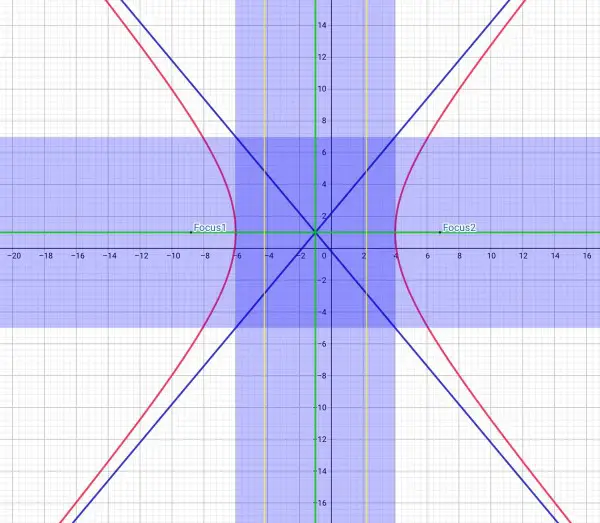
The conic is a hyperbola, and its equation can be written (x+1)²/25-(y-1)²/36=1. a²=25, b²=36, so the length of the semixaxis (transverse) is 5, length of the semiaxis (conjugate) is 6. The dark shaded blue rectangle shows the axes.
Centre is (-1,1) where the axes (green) intersect.
Horizontal transverse axis length is 10, vertical conjugate axis is length 12 (dimensions of the central rectangle).
The foci and directrices (yellow) are shown. Focal distance c=√(5²+6²)=√61, to left and right of the centre. Directrices are x=±a²/c=±25/√61 relative to the centre at (-1,1).
Asymptotes are in blue. Equations are 6x+5y+1=0, 6x-5y+11=0 which are found from (x+1)²/25=(y-1)²/36.