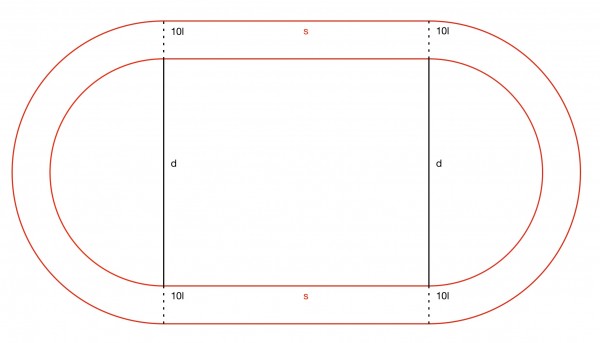
The running track is enclosed in red. The inner dimensions must give us the track length of 300m for the runner in lane 1 (innermost). So πd+2s=300. The area of the central plot is sd+πd²/4 and the area of the whole track including the central plot is s(d+20l)+π(d+20l)²/4.
The track area itself is the difference between these two areas:
20ls+10πl(d+10l). We know l=1.2m (lane width), and s=½(300-πd), if we assume that lane 1 has a total length of 300m. If we insert the known values we get:
24s+12π(d+12)=12(300-πd)+12π(d+12)=3600+144π=4052.39 sq m approx.
We need the answer in square feet. 1ft=0.3048m, so 1sq ft=0.0929sq m approx. 4052.39sq m=43619.6 sq ft approx.