Question

Find the distance between points A and B, located on the opposite shores of a river, if on one of the shores following segments have been drawn and measured SB=60m, SC=80m, SD=180m and BC∥AD. 

Comments

You need to supply a diagram. If BC is parallel to AD, then C must be on the same shore as A, but that is contrary to the statement that all the segments are on the same shore, that is, the opposite shore to A, since SB is on that shore and B is opposite to A. Perhaps you could rephrase the question.

Answer 1

 

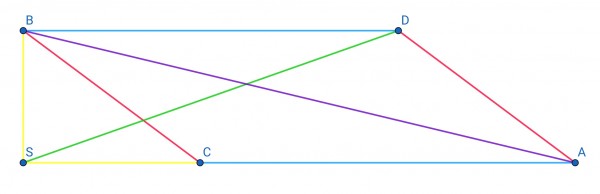
Since AD is parallel to BC (red lines) and A and B are on opposite shores, the points C and S are on the A shoreline. If C, D and S were all on the B shoreline, BC would be a segment on the B shore, and AD could not be parallel to BC. Therefore, the given segments could not all be on the same shoreline. The diagram represents what I believe to be the situation, assuming the shorelines are parallel, so blue segments BD and CA are also parallel, and ACBD is a parallelogram. 

To provide a unique solution I’ve assumed the yellow segments SB and SC are perpendicular, meaning that point S is exactly opposite point B on the A shore. If S were not directly opposite B there would be more than one solution, that is, AB could have a number of different lengths (see later).

From the diagram:

BD²=SD²-SB² (Pythagoras) and CA=BD, so BD=√(180²-60²)=60√(9-1)=120√2 metres. By Pythagoras:

AB²=SB²+SA²,

AB²=SB²+(SC+CA)²=

60²+(80+120√2)²=

3600+6400+28800+19200√2=

38800+19200√2=65952.9m² approx.

Therefore AB=√65952.9=256.81m approx.

It can be shown that if the bearing of B from the point S is θ degrees, that is, SB is angle θ to SA, AB=√[3600sin²θ+(80-60(√(9-sin²θ)-2cosθ))²] metres. As θ decreases to 0 or increases to 180°, the distance between opposite shores decreases and AB varies between 140m (θ→0) and 380m (θ→180°).