I 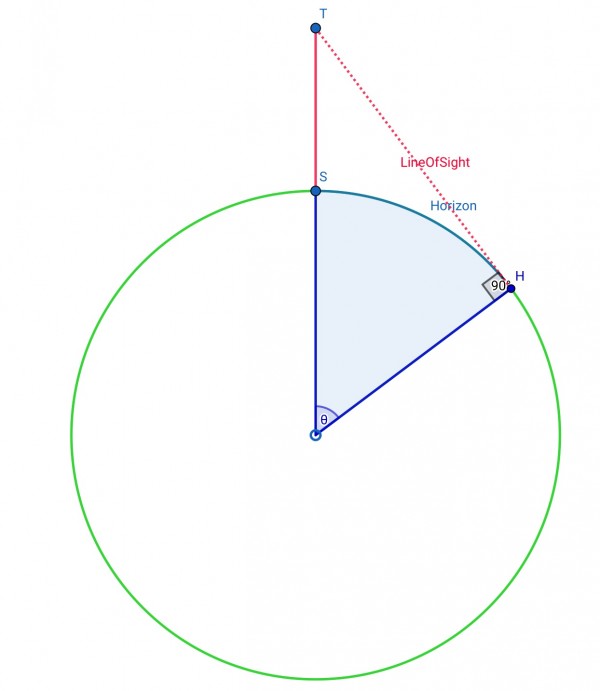
Consider the geometry. The picture shows the tower TS above sea level (S) in red, the globe (centre O) in green, with radii SO and HO in blue. The line of sight TH from the top of the tower T to the observed horizon H is shown as a dotted red line TH. The horizon distance is the arc SH, which subtends angle θ (=∠TOH=∠SOH). TH is a tangent at H to the globe, so ∠THO is a right angle.
Let’s look at the problem algebraically:
h=TS, SO=HO=R, arc SH=Rθ.
cosθ=OH/TO=R/(R+h), from which θ=arccos(R/(R+h)).
So the apparent horizon distance z=Rarccos(R/(R+h)).
R=6378000, h=72, θ=arccos(6378000/6378072)=0.004751568 radians approx.
A simple way to find the variation in θ is to work out the maximum and minimum values of R/(R+h). If the error in R is ∆R and the error in h is ∆h, we have the following values for R/(R+h):
(R-∆R)/(R-∆R+h-∆h)=0.9999890029,
(R-∆R)/(R-∆R+h+∆h)=0.9999883745 (min), θ=0.00482193374 (max),
(R+∆R)/(R+∆R+h-∆h)=0.9999890468 (max), θ=0.00468043175 (min),
(R+∆R)/(R+∆R+h+∆h)=0.9999884209.
From these we can work out z and its error:
z=Rθ:
z=29911.49, 30692.78m or 29.91149, 30.69278km
Reducing this to 2 decimal places:
horizon is 30.30±0.39km.