The equation of the cone is z²=x²+y². This is in fact a diabolo, which is two cones joined at their apices.
Consider a sphere, centre B(1,2,0) and radius r. Equation is:
(x-1)²+(y-2)²+z²=r².
If r is such that the sphere touches the cone at A without intersecting it, then at the point of contact, the tangent of the sphere will be equal to the tangent of the cone at the contact point A. The radius of the sphere will be the shortest distance between B and A.
We can find the orthogonal gradients of the two solids:
Cone: 2z∂z/∂x=2x, ∂z/∂x=x/z; 2z∂z/∂y=2y, ∂z/∂y=y/z.
Sphere: 2(x-1)+2z∂z/∂x=0, ∂z/∂x=(1-x)/z and ∂z/∂y=(2-y)/z.
When these gradients are the same:
x/z=(1-x)/z, 2x=1, x=½; y/z=(2-y)/z, 2y=2, y=1.
Therefore we can find r:
z²=x²+y²=¼+1=5/4;
(-½)²+(-1)²+z²=r²,
¼+1+5/4=r², r=√(5/2).
So we have A(½,1,√5/2) and AB=r=√(5/2). There is a complementary point on the other half of the diabolo (z=-√5/2), but r is the same by symmetry.
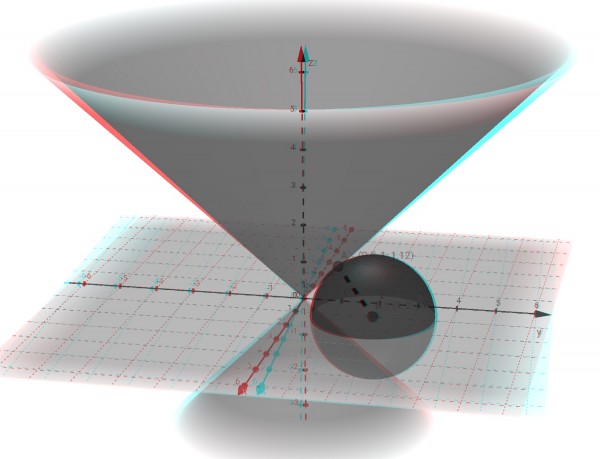
The above image can be viewed with 3D glasses (right lens is green or blue, left lens is red). The image shows only the join to the upper cone of the diabolo.