F(A,B,C,D) = A’B’C’D’ + A’B’C’D + A’BCD + ABCD + AB’CD + A’B’CD + AB’C’D’ + AB’CD’ +A’BC’D + ABCD’

Question

(A)Simplify F in SOP form with 7 literals only.

(B)Draw the logic diagram of the simplified F in SOP form referring to letter A.

Answer 1

TRUTH TABLE FOR F

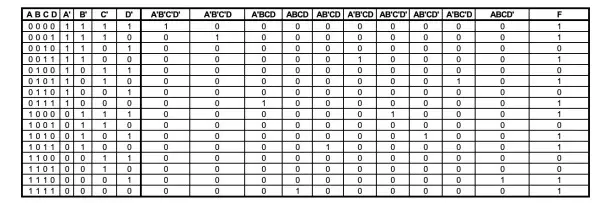
Now we need to find minTerms to correspond to the ten 1s in the F column. The Boolean sum of the following SOP products equals 1. Each term is derived from the row number. For example, starting with r₀=0000 as row 1 and r₁₅=1111 as row 16 in the table, r₅=0101 (row 6) and we use the complement instead of the true literal wherever there is a zero, so 0101=A'BC'D.

F=A'B'C'D'+A'B'C'D+A'B'CD+A'BC'D+A'BCD+AB'C'D'+AB'CD'+AB'CD+ABCD'+ABCD, which is the canonical (standard) SOP expression, corresponding to the given expression, the order of terms being indicated in the truth table. The colour-coding suggests how some terms may be simplified by grouping, because the Boolean x+x'=1 (a literal OR its complement=1).

Alternatively, F=A'B'C'D'+A'B'C'D+A'B'CD+A'BC'D+A'BCD+AB'C'D'+AB'CD'+AB'CD+ABCD'+ABCD.

The simplifications are:

(1) F=A'B'C'(D'+D)+A'CD(B'+B)+A'BC'D+AB'C'D'+AB'C(D'+D)+ABC(D'+D),

F=A'B'C'+A'C'D+A'BC'D+AB'C'D'+AB'C+ABC,

F=A'C'(B'+D)+C'(A'BD+AB'D')+AC,

F=C'(A'(B'+D+BD)+AB'D')+AC,

F=C'(A'(B'+D(1+B))+AB'D')+AC, (1+B=1 for any B)

F=C'(A'(B'+D)+AB'D')+AC=C'(B'(A'+AD')+A'D)+AC by rearrangement.

(2) F=A'B'C'D'+A'B'C'D+A'B'CD+A'BC'D+A'BCD+AB'C'D'+AB'CD'+AB'CD+ABCD'+ABCD, 

F=A'B'C'+A'B'CD+A'BD+AB'C'D'+AB'C+ABC,

F=A'B'C'+A'B'CD+A'BD+AB'C'D'+AC,

F=A'(B'(C'+CD)+BD)+A(B'C'D'+C).

(1) uses only 7 distinct literals, while (2) uses all 8. 

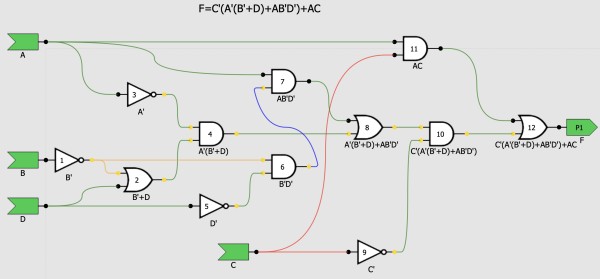
(B) CIRCUIT DIAGRAM OF F=C'(A'(B'+D)+AB'D')+AC