A train leaves a station and travels north at a speed of 45 mph. Four hours later, a second train leaves on a parallel track and travels north at 105 mph. How far from the station will they meet?

Question

It’s a college algebra question

Answer 1

The distance s₁ the first train travels in time t₁ is 45t₁. The second train travels distance s₂=105t₂ in time t₂.

Because the second train leaves 4 hours later than the first, t₁-t₂=4, so t₂=t₁-4 if we measure time with reference to t₁. Therefore s₂=105(t₁-4). When the second train catches up with the first, they are at the same distance (s) from their starting points at the same time (t), so:

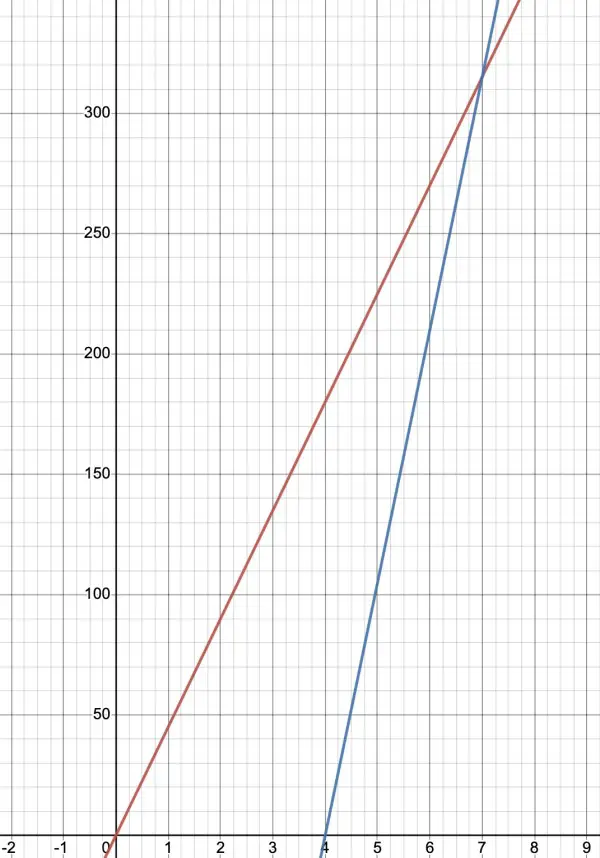
45t=105(t-4), 3t=7(t-4) when we divide each side by 15, 3t=7t-28, 4t=28, t=7hr and s=45t=315 miles.

This is graphically represented below where the path of the first train is shown in red and the second in blue. Distance (miles) is measured on the vertical axis and time (hours) on the horizontal axis. The graph shows that the first train has already travelled 180 miles when the second train starts off. The tracks intersect at (7,315), that is, at 7 hours and 315 miles (each distance subdivision is 10 miles).