x2+9y2-4x+54y+49=0 can be written:
x2-4x+9(y2+6y)+49=0.
Complete the squares for x and y:
x2-4x+4+9(y2+6y+9)+...
We have added two constants: 4 and 9×9=81, 4+81=85. This needs to be added to the right hand side to balance the equation:
x2-4x+4+9(y2+6y+9)+49=85. Now rewrite the equation:
(x-2)2+9(y+3)2=85-49=36.
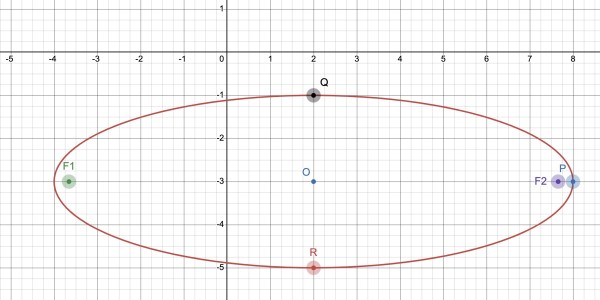
This is the equation of an ellipse with axial centre O(2,-3) (x-2=0⇒x=2; y+3=0⇒y=-3).
We can write this as: (x-2)2/36+(y+3)2/4=1, which is the standard form for an ellipse. The semimajor axis is a=√36=6 and the semiminor axis is b=√4=2.
The semi-axes cross at the centre of the ellipse and the foci lie on the line joining the extreme horizontal points of the ellipse.
The extreme left is 6 units to the left of the centre and the extreme right is 6 units to the right. The extreme verticals are 2 units above and below the centre.
Let's consider the extreme left at (-6,0) if the centre was at (0,0) and the extreme right is (6,0). Let's say that the foci are at (-c,0) and (c,0) with this repositioned centre. We can adjust coordinates later with respect to the origin of the graph at (0,0); but for now it's easier to think of the ellipse with its centre at (0,0).
An ellipse is formed when the sum of the distances between any point on the ellipse and its foci are constant. So if pick a point P(a,0) (right extreme) then the geometry tells us that:
6-c=distance between P and the right focus, and 6+c=distance between P and the left focus.
Therefore the constant=6-c+C+c=12.
Pick a point Q(0,2) or R(0,-2) (highest and lowest points with respect to the centre). Using Pythagoras:
√(22+c2)=distance between Q and R from either focus, and the sum of these two distances=2√(22+c2), which is the constant 12.
So 2√(22+c2)=12,
√(22+c2)=6,
4+c2=36, c2=32, c=√32=4√2.
The focus is 4√2 units on either side of the centre on the major axis (x), which is (2,-3).
The foci (F2 and F1) are therefore (2+4√2,-3) and (2-4√2,-3).