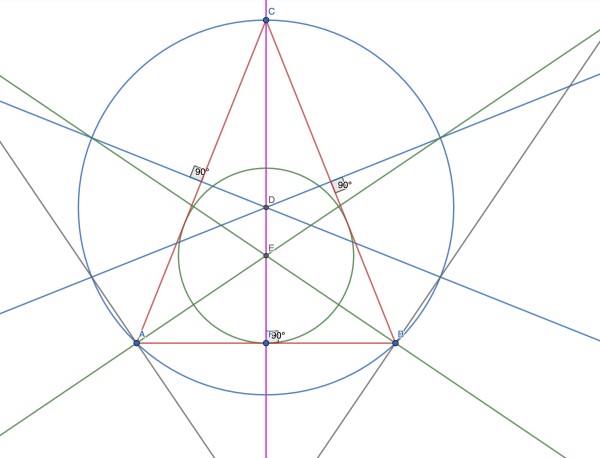
The centre of the inscribed circle is at the intersection of the angle bisectors, while the centre of the circumscribed circle is at the intersection of the medians (side bisectors). In an isosceles triangle these centres lie on the perpendicular from the apex to the base, where the base is not one of the equal sides.
The figure below shows isosceles triangle ABC (equal side lengths AC and BC) with its circumcircle (blue) and incircle (green) with medians (blue) and angle bisectors (green). The vertical pink line is both a median and an angle bisector and it contains the centres D and E of the circumcircle and incircle respectively. d=DE is the distance between their centres.
CD=r and EF=p. (C, D, E, F are collinear.)
The formula 1/p=1/(r-d)+1/(r+d) (see later for my solution for the isosceles triangle) can be used to find the distance between the centres of the incircle and circumcircle for any triangle.
Multiply through by p(r2-d2):
r2-d2=pr+pd+pr-pd=2pr. Therefore d2=r2-2pr=r(r-2p), and d=√[r(r-2p)], which is what was to be proved.
For proof see https://www.cut-the-knot.org/triangle/EulerIO.shtml.
Here is my solution using a greatly simplified picture:
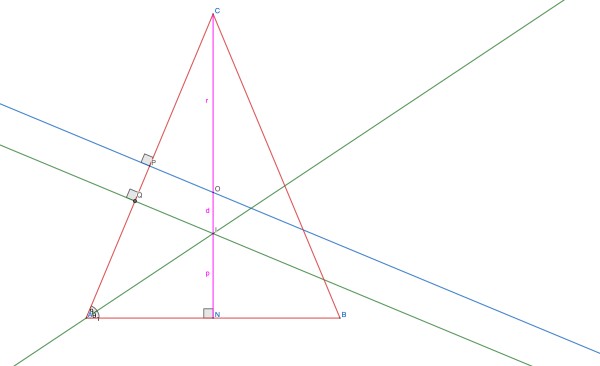
Because of symmetry, we only need to focus on triangle CAN which contains essential elements, omitting the circles. Note angle θ=QÂI=IÂN (because angle A is bisected). I is the centre of the incircle while O is the centre of the circumcircle.
Right triangles AIN and AIQ are congruent, so QI=IN=p and AQ=AN. Right triangles COP, CAN and CIQ are similar. CÔP=CÎQ=CÂN=2θ.
We should be able to work out other lengths in terms of r, d, p and θ. And we should also be able to work out θ, or its trigonometric ratios in terms of r, d and p. This should enable us to establish a relationship between r, d and p without θ.
sin(θ)=IN/AI=QI/AI=p/AI (triangles AIN and AIQ),
sin(2θ)=CN/CA=(r+d+p)/CA=(r+d+p)/CA (triangle CAN),
sin(2θ)=CP/CO=CP/r, and CA=2CP (triangle COP),
sin(2θ)=CQ/CI=(CA-QA)/(r+d) (triangle CIQ).
tan(θ)=IN/AN=QI/QA=p/QA, QA=AN=pcot(θ).
Trig identity: sin(2θ)=2sin(θ)cos(θ).
What we've discovered so far enables us to determine θ in terms of the three measures r, d and p, because in triangle CIQ we have two sides CI=r+d and QI=p. So we have the ratio QI/CI=cos(2θ)=p/(r+d).
We have three similar triangles COP, CAN and CIQ from which we can see three equations for cos(2θ), just as we did for sin(2θ):
Triangle CAN: cos(2θ)=AN/CA=AN/(2CP),
Triangle COP: cos(2θ)=OP/CO=OP/r,
OP doesn't seem to be defined other than as rcos(2θ). However, note that CQ=CA-QA, and QA=pcot(θ)=p/tan(θ). And we can derive tan(θ) from cos(2θ) and the result will be terms involving r, d and p only. cos(2θ)=2cos2(θ)-1 or 1-2sin2(θ) (trig identity), from which:
cos2(θ)=(1+cos(2θ))/2=½(r+d+p)/(r+d); 2sin2(θ)=1-cos(2θ)=1-p/(r+d)=(r+d-p)/(r+d).
CA=2CP=2rsin(2θ), CQ=2rsin(2θ)-pcot(θ), so:
sin(2θ)=(2rsin(2θ)-pcot(θ))/(r+d) (triangle CIQ).
Expanding the double angles and substituting cot(θ)=cos(θ)/sin(θ):
2sin(θ)cos(θ)=(4rsin(θ)cos(θ)-(pcos(θ)/sin(θ)))/(r+d),
2sin(θ)=(4rsin(θ)-(p/sin(θ)))/(r+d), so 2sin2(θ)=(4rsin2(θ)-p)/(r+d) (multiplying through by sin(θ)).
That is: r+d-p=2r(r+d-p)/(r+d)-p, r+d=2r(r+d-p)/(r+d) (the denominator r+d from substitution of 2sin2(θ) is the same on both sides of the equation, so the numerators must be equal).
(r+d)2=2r2+2rd-2rp, r2+2rd+d2=2r2+2rd-2rp, d2=r2-2rp=r(r-2p), d=√(r(r-2p)) QED.
2rp=r2-d2, 1/(2rp)=1/(r2-d2), 1/p=2r/(r2-d2)=A/(r+d)+B/(r-d) (partial fractions).
Ar-Ad+Br+Bd=2r, A+B=2, -A+B=0, so A=B=1 and 1/p=1/(r+d)+1/(r-d).
(Although we started with an isosceles triangle, this formula applies to all triangles.)