A cube has edges of length 3ft. Point A is the midpoint of an edge. Find the measure of angle ABC.

Question

There is a cube with a triangle inside and point A is the midpoint. The edges are 3ft long. I need to find the measures of angles A, B and C.

Answer 1

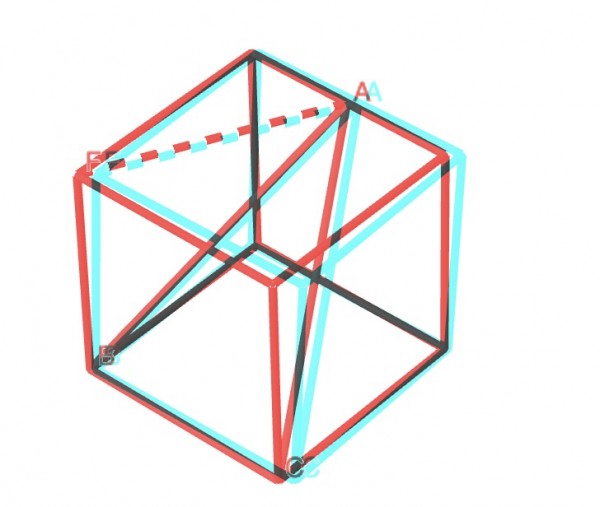
Above is what I think you mean (in 3D, which can be viewed with 3D filters, blue/green right eye, red left eye). The broken line is a construction line for the purposes of obtaining a solution. The length of the side of the cube is irrelevant since all cubes are similar figures and we are measuring angles, not actual lengths, and angles are ratios of lengths.

We need to find the lengths of AB and AC in the isosceles triangle ABC. Then we can find all the angles of the triangle.

In right triangle AFB, AF²+FB²=AB², and we can find AF because it's the hypotenuse of the right triangle formed by AF and the top corner of the cube.

If we represent the side of the square as a (=3ft), AF²=(a/2)²+a²=5a²/4 (=45/4ft²). I'll work with algebra and actual lengths for comparison. FB=a so:

5a²/4+a²=AB², making AB²=9a²/4, AB=3a/2 (=4.5ft). AC=AB=3a/2 because ABC is isosceles. If we drop a perpendicular from A to BC it bisects BC and also bisects angle A.

cosB=cosC=(a/2)/AB=(a/2)/(3a/2)=1.5/4.5=⅓. So measure of B, C=arccos(⅓)=70.5288° approx. Therefore A=180°-(B+C)=38.9424°.