f(x)=k-5(x-2)2 and g(x)=x2+px+3,find value of p?

Question

Two quadratic functions f(x)=k-5(x-2)2 and g(x)=x2+px+3, both intersecting at x-axis. Find the value of p.

Answer 1

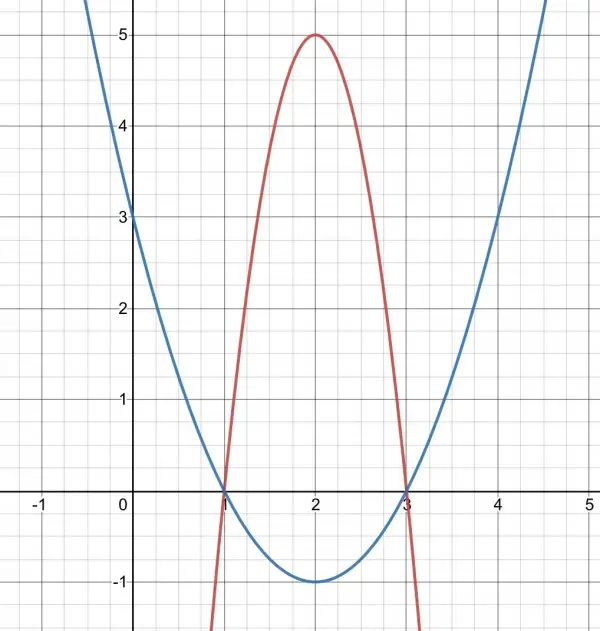
f(x) is an inverted U shape while g(x) is an upright U shape. f(x) has a vertex at (2,k) and it intersects the x-axis when y=0, that is, 5(x-2)²=k, x=2±√(k/5). These are the intersection points for g(x) so x²+px+3=0 when x=2±√(k/5).

The solution for x when g(x)=0 is given by the quadratic formula: x=(-p±√(p²-12))/2. These values of x must coincide with the intersection points for f(x), 

therefore, -p/2=2, p=-4. 

We can also find k: √(p²-12)/2=√(k/5). p²=16, so 1=√(k/5), k=5.

f(x)=5-5(x-2)², g(x)=x²-4x+3.