Determine the period,phase shift,range,and amplitude of y=3cos(x+2pi/3)-2?

Question

sketch one cycle of the graph of each function.

Answer 1

Phase shift formula=AT((2π/P)(x-ω))+V,

where A is the amplitude, P=period, ω=phase shift, V=upward vertical shift, and T is a trigonometric function (usually sin or cos). 2π/P is the frequency, η, the number of cycles in the period 2π, so Pη=2π.

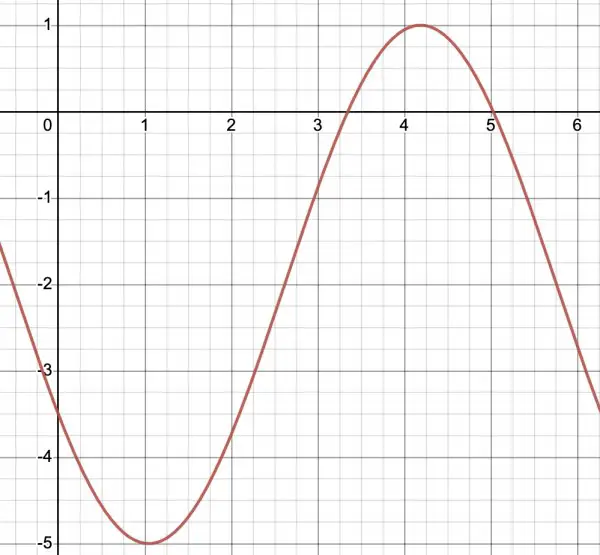
For 3cos(x+2π/3)-2, A=3, P=2π, ω=-2π/3 radians, V=-2.

To find the range we replace cos(x-2π/3) with ±1. This gives us a low of -3-2=-5 and a high of 3-2=1.

The range is [-5,1] and the magnitude of the range is twice the amplitude=2A=6.