y=5x²-40x+78,
y=5(x²-8x+16-16)+78,
y=5(x-4)²-80+78,
y+2=5(x-4)² is standard form: y-k=a(x-h)².
Parabola with vertex at (h,k)=(4,-2).
The focus lies on the line x=4.
The axes of the parabola are x=4 and y=-2. Relative to these axes the vertex is at (0,0) and the focus is at F(0,c) and the directrix line is y=-c, where c is a constant to be found. The equation relative to the parabola’s axes is y=5x².
All points P(x,y) on the parabola are a distance PF from the focus and, if we drop a perpendicular PN from P onto the directrix line y=-c, we can use the fact that PF=PN for all points P (definition of any parabola). Considering the parabola as y=5x²:
PF=√((y-c)²+x²) and PN=y+c, therefore y+c=√((y-c)²+x²) for any P(x,y) on the parabola.
Squaring both sides:
y²+2cy+c²=y²-2cy+c²+x², 4cy=x², or y=x²/4c; but y=5x², so y/5=x², and 4c=1/5, making c=1/20. So we have the focus F(0,1/20) and directrix line y=-1/20 relative to the parabola’s axes.
That places the focus, relative to the normal axes, at F(h,k+c)=F(4,-2+1/20).
So F(4,-39/20) is the actual focus. The directrix line is y=k-c=-2-1/20=-41/20.
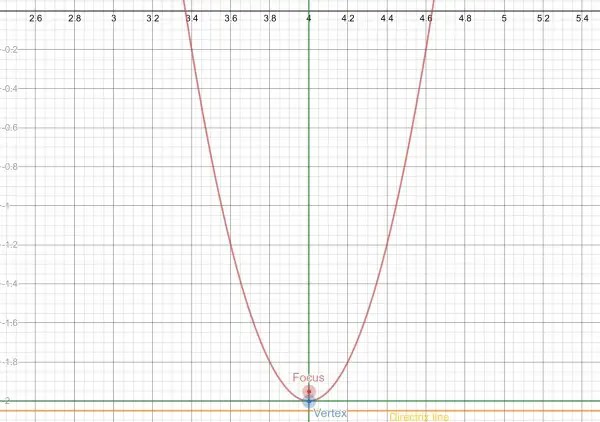
The axes of the parabola are shown in green.