In the venn diagram,M and N are intersecting sets in the universal set U.

Question

MnN=6

(MuN)'=6

(MnN')=8x+4

(M'nN)=2x+7

a)Express n(M) and n(N) in terms of x

b).Given that n(M)=n(N),find the

ii)value of x

ii)n(u)

Answer 1

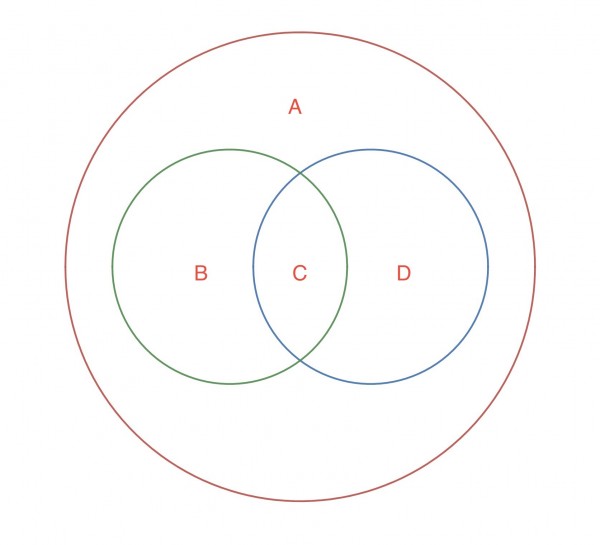
The above diagram shows four Venn regions A-D. The large red circle represents the universal set U. The green circle represents set M and the blue circle represents N. We can relate the intersections and unions to the regions. So M=B+C, N=C+D, U=A+B+C+D. M⋂N=C, M'=A+D, N'=A+B. I have assumed that the prime (') means NOT-X where X is the name of the set, hence N' means NOT-N, that is, the regions not including N.

M⋃N=B+C+D, (M⋃N)'=A, M⋂N'=[B+C]⋂[A+B]=B, M'⋂N=[A+D]⋂[C+D]=D.

For the next part I assume that the numbers and expressions are set sizes.

So now we can put in some values:

M⋂N=C=6

(M⋃N)'=A=6

M⋂N'=B=8x+4

M'⋂N=D=2x+7

a) n(M)=n(B+C)=8x+4+6=8x+10; n(N)=n(C+D)=6+2x+7=2x+13.

b) (i) n(M)=n(N)⇒8x+10=2x+13, 6x=3, x=½. [n(M)=n(N)=14.]

(ii) n(A+B+C+D)=n(U)=6+8x+4+6+2x+7=10x+23=28.

Or, n(U)=n(M)+n(N)-n(M⋂N)+A=14+14-6+6=28.