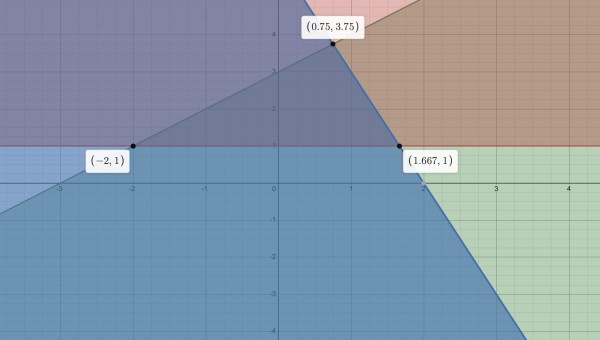
First we need to find where the regions intersect.
y=1 intersects y=x+3, that is, when x+3=1, x=-2, so the intersection point is (-2,1).
y=1 intersects 3x+y=6, that is, 3x+1=6, 3x=5, x=5/3, so the intersection point is (5/3,1).
y=x+3 intersects 3x+y=6, when 6-3x=x+3, 4x=3, x=¾, y=15/4, so the intersection is (¾,15/4).
The inequalities confine the region inside the triangle (-2,1), (¾,3¾), (1⅔,1) (feasible region), including its sides. For less than inequalities the shading is below the line graph; for greater than equalities the shading is above the line graph, hence the enclosed region.
We just need points within the triangle (including its sides) which are whole numbers, which are:
(-2,1), (-1,1), (0,1), (1,1), (-1,2), (0,2), (1,2), (0,3), (1,3). These points are working from the base of the triangle to its apex. Note that each inequality is satisfied.
So the corresponding x+y values are:
-1, 0, 1, 2, 1, 2, 3, 3, 4.
Removing duplicates we have: -1, 0, 1, 2, 3, 4.
The greatest value is 4 and the least is -1.
(HINT: A graph helps because there are only two variables. With more than two variables perhaps the Simplex Method would be better.)
The feasible region is the darkest shading.